Не знаю, как лет двадцать назад, но если говорят решить уравнение, значит нужно найти его корни, например, выраженные через радикалы.
Если операция извлечения корня элементарна, то вот одно из решений.
Итак, доказываем, что


Поскольку нужно рассматривать только отрезок
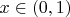
, то

Докажем, что


На указанном отрезке

Выясним, когда

. Это случится при

Значит нужно рассматривать лишь промежуток
![$x\in[\frac{2}{3},(\frac{1}{5})^{1/7}]$ $x\in[\frac{2}{3},(\frac{1}{5})^{1/7}]$](https://dxdy-03.korotkov.co.uk/f/6/6/9/669ad434ca1bfa3c43bd30c6ac34cd7082.png)
.
Имеем

Выясним, когда

. Находим

.
Значит можно рассматривать
![$x\in[\frac{2}{3},(\frac{2}{23})^{1/7}]$ $x\in[\frac{2}{3},(\frac{2}{23})^{1/7}]$](https://dxdy-04.korotkov.co.uk/f/3/5/a/35a28977f67ab169a37ff3d2592b522482.png)
.
Имеем

Выясним, когда

. Находим

. Но эта точка не принадлежит рассматриваемому отрезку.