Я встретил препятствие на пути осуществления этого плана, который состоял в том, чтобы в предположении:

найти такое простое число

, что

не является квадратичным вычетом по модулю никакого простого делителя числа

, а уравнение:
(58)

,
где
![$c=x^2-\sqrt[3]{4} yz$ $c=x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/a/2/f/a2f3e2b75e4e774dbb60904d89e8e97982.png)
или
![$c=(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$ $c=(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$](https://dxdy-01.korotkov.co.uk/f/0/e/7/0e7c1d778ae454b1083e1cd9c622082982.png)
,
имеет ненулевое решение в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
для одного из этих значений числа

.
Я доказал, что уравнение (58) имеет ненулевое решение, но препятствие заключается в том, что числа

и

могут иметь общий делитель, который является также делителем числа

, и этот общий делитель может быть идеалом, на который равенство (58) нельзя сократить, и непонятно, как из этого равенства получить противоречие.
Тем не менее, сформулируем гипотезу и докажем, что уравнение (58) имеет ненулевое решение, с тем чтобы можно было к этому вернуться, если появятся новые идеи.
Гипотеза A
----------------
Пусть

,

, ...,

- нечётные простые числа, не равные

.
Существует нечётное простое число

, не равное

-ём и дающее остаток не равный

при делении на

, такое, что

не сравнимо с квадратом по модулю любого из простых чисел

,

, ...,

(в частности,

не равно ни одному из этих чисел), и
![$\sqrt[3]{2}-1$ $\sqrt[3]{2}-1$](https://dxdy-03.korotkov.co.uk/f/e/f/8/ef8de88e5ab179b5c68a30a7db009ffb82.png)
не сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Лемма 12
-------------
Пусть

- произвольный нечётный простой идеал кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
, и пусть

и
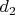
- произвольные элементы этого кольца, не делящиеся на

.
Тогда уравнение

имеет решение

в

-адических числах кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
Доказательство или ссылка на доказательство этой леммы будут даны в дальнейшем.
Лемма 13
-------------
Пусть

, где

,

,

,

- целые числа, число

взаимно-просто с

,

- нечётное число и число

не делится на 3.
Тогда числа
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
и
![$x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$ $x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$](https://dxdy-01.korotkov.co.uk/f/8/5/2/852874cd70d36b63b7155b048f9795fe82.png)
взаимно-просты.
Доказательство:
-----------------------
Предположим:
(59) числа
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
и
![$x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$ $x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$](https://dxdy-01.korotkov.co.uk/f/8/5/2/852874cd70d36b63b7155b048f9795fe82.png)
делятся на простой идеал

.
В силу тождества

, из (59) следует:
(60) число
![$3 (\sqrt[3]{4} yz)^2$ $3 (\sqrt[3]{4} yz)^2$](https://dxdy-04.korotkov.co.uk/f/f/7/4/f74bae7c165f17ccb4851a13cd748d6c82.png)
делится на

.
В силу равенства
![$(x^2-\sqrt[3]{4} yz)(x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2)=a^2$ $(x^2-\sqrt[3]{4} yz)(x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2)=a^2$](https://dxdy-04.korotkov.co.uk/f/3/2/b/32b0b562907d0f6c118ad641fa3a5f4882.png)
и поскольку число

не делится на

и на

, то числа

и

не делятся на

, и из (60) следует:
(61) число

делится на

.
Из (59) и (61) следует, что

делится на

, что противоречит взаимной простоте чисел

и

.
Значит предположение (59) неверно, и числа
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
и
![$x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$ $x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$](https://dxdy-01.korotkov.co.uk/f/8/5/2/852874cd70d36b63b7155b048f9795fe82.png)
взаимно-просты.
Что и требовалось.
Сформулируем теорему, которую я не смог доказать из-за препятствия, о котором шла речь выше:
Теорема 1
--------------
Пусть

, где

,

,

,

- целые числа, число

взаимно-просто с

,

- нечётное число и число

не делится на 3.
Если гипотеза А верна, то одно из чисел
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
и
![$(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$ $(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$](https://dxdy-02.korotkov.co.uk/f/1/2/1/121183d956d35c807c98113f2084809382.png)
является квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
Вместо этой теоремы, докажем, что уравнение (58) имеет ненулевое решение.
Лемма 14
-------------
Пусть

, где

,

,

,

- целые числа, число

взаимно-просто с

,

- нечётное число и число

не делится на 3.
Пусть

- простое число, не равное

-ём, дающее остаток не равный

при делении на

, и такое, что
![$\sqrt[3]{2}-1$ $\sqrt[3]{2}-1$](https://dxdy-03.korotkov.co.uk/f/e/f/8/ef8de88e5ab179b5c68a30a7db009ffb82.png)
не сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Пусть

не является делителем числа

.
Тогда уравнение:
(62)

имеет ненулевое решение в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
для одного из значений числа

:
![$c=x^2-\sqrt[3]{4} yz$ $c=x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/a/2/f/a2f3e2b75e4e774dbb60904d89e8e97982.png)
или
![$c=(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$ $c=(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$](https://dxdy-01.korotkov.co.uk/f/0/e/7/0e7c1d778ae454b1083e1cd9c622082982.png)
.
Доказательство:
---------------------
Пусть

- такое целое число, что

делится на

.
По условию:
(63)
![$\sqrt[3]{2}-1$ $\sqrt[3]{2}-1$](https://dxdy-03.korotkov.co.uk/f/e/f/8/ef8de88e5ab179b5c68a30a7db009ffb82.png)
не сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Согласно лемме 11, из (63) следует:
(64)

не является квадратичным вычетом по модулю

.
Из (64) следует:
(65) одно из чисел

и

является квадратичным вычетом по модулю

.
Cогласно лемме 7 и лемме 9, из (65) следует:
(66) одно из чисел
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
и
![$(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$ $(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$](https://dxdy-02.korotkov.co.uk/f/1/2/1/121183d956d35c807c98113f2084809382.png)
сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Обозначим через

то число из чисел
![$x^2-\sqrt[3]{4} yz$ $x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2382cb9b33d6ed7dbe22cf60fc3d734c82.png)
и
![$(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$ $(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$](https://dxdy-02.korotkov.co.uk/f/1/2/1/121183d956d35c807c98113f2084809382.png)
, которое сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Имеем:
(67) число

сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Если
![$c=x^2-\sqrt[3]{4} yz$ $c=x^2-\sqrt[3]{4} yz$](https://dxdy-03.korotkov.co.uk/f/a/2/f/a2f3e2b75e4e774dbb60904d89e8e97982.png)
, пусть
![$d=x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$ $d=x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2$](https://dxdy-02.korotkov.co.uk/f/1/e/e/1ee4c905b28cc78c34f94a9dab837c9982.png)
.
Если
![$c=(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$ $c=(\sqrt[3]{2}-1)(x^2-\sqrt[3]{4} yz)$](https://dxdy-01.korotkov.co.uk/f/0/e/7/0e7c1d778ae454b1083e1cd9c622082982.png)
, пусть
![$d=((\sqrt[3]{2})^2+\sqrt[3]{2}+1)(x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2)$ $d=((\sqrt[3]{2})^2+\sqrt[3]{2}+1)(x^4+x^2 \sqrt[3]{4} yz+(\sqrt[3]{4} yz)^2)$](https://dxdy-01.korotkov.co.uk/f/0/2/b/02b2e64f3ea8203c74725184c953f1bc82.png)
.
Имеем:
(68)

В силу леммы 13:
(69) числа

и

взаимно-просты.
Из (67) и (68) следует:
(70) число

сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Из (67) следует:
(71) для любого натурального числа

: число

сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Из (70) следует:
(72) для любого натурального числа

: число

сравнимо с квадратом в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Докажем, например, (71) по индукции.
При
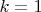
: (71) верно в силу (67).
Предположим, для какого-либо натурального числа

:
(73) число

сравнимо с

в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

.
Тогда:
(74) число

сравнимо с

в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
по модулю

, где
число
![$t \in \mathbb{Z}[\sqrt[3]{2}]$ $t \in \mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-01.korotkov.co.uk/f/8/c/4/8c4f6425675800a51b4df266149fb20d82.png)
сравнимо с

по модулю

.
Такое число

существует, так как число

взаимно-просто с

, в силу (73), (68) и поскольку число

не делится на

.
Рассмотрим уравнения:
(75)

и
(76)

,
где

,

,

- неизвестные.
Пусть

- какой-либо простой нечётный идеал кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
Если

делится на

, то уравнения (75) и (76) имеют ненулевые решения (с

) в

-адических числах кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
, в силу (71) и (72).
Предположим теперь, что

не делится на

.
В силу (69) одно из чисел

и

не делится на

.
Пусть, например,

не делится на

.
Тогда, в силу леммы 12:
(77) число

представимо в виде

,
где

и

-

-адические числа кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
Из (77) и (68) следует:
(78) число

представимо в виде

,
где

и

-

-адические числа кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
Значит:
(79) для любого нечётного идеала

, уравнения (75) и (76) имеют ненулевые решения (с

) в

-адических числах кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
Поскольку

и

- положительные числа, то:
(80) уравнения (75) и (76) имеют ненулевые решения (с

и

) в действительных числах.
В силу формулы произведения символов Гильберта:
(81) уравнения (75) и (76) имеют ненулевые решения в

-адических числах кольца
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
для единственного чётного простого идеала этого кольца:
![$\rho=(\sqrt[3]{2})$ $\rho=(\sqrt[3]{2})$](https://dxdy-03.korotkov.co.uk/f/a/1/0/a1071f2e8c25ce926b2a821dabb2c4f082.png)
.
Из (79), (80), (81) и локально-глобального принципа Хассе следует:
(82) Уравнения (75) и (76) имеют ненулевые решения в кольце
![$\mathbb{Z}[\sqrt[3]{2}]$ $\mathbb{Z}[\sqrt[3]{2}]$](https://dxdy-03.korotkov.co.uk/f/6/d/7/6d7a3a65b47554ddcce081cd5bce704082.png)
.
Что и требовалось.