Как доказать, понятия не имею. Подскажите, каким методом доказываются подобные вещи?
Количество циклов посчитал:
НОД

, таких будет (целая часть от деления 87 на 3) - 28 штук по 3 цикла.
далее
НОД

- еще 2 штуки по 29 циклов.
В итоге:
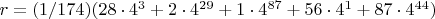
преобразуем

находим остатки от деления



Рассуждения: т.к. 2 в любой степени и 87 взаимно просто,

т.к. 56 - ф-ция Эйлера от 87


Для 173 аналогичные рассуждения.

Суммируем остатки,

. То есть делиться на 87 без остатка.
Получилось натуральное число. Это конечно не говорит о правильности.. Но если бы не поделилось нацело, то уж точно не правильно.