(ко)гомология

[alcoholist]

xmaister в сообщении #699219 писал(а):

Т.е. это просто такое обозначение?

Нет, указанный мною изоморфизм надо еще установить

xmaister в сообщении #699321 писал(а):

Это правильно?

нет

[xmaister]

$H_0(\mathbb{R};R)$ сводится к нахождению фактора свободного модуля с множеством образующих $S$ по подмодулю, состоящего из элементов вида $M=\left\{\sum\limits_{i=1}^{k}m_i(t_i-t_i')|t_i,t_i'\in S,m_i\in R\right\}$. Получается, что $H_0(\mathbb{R},R)\cong R$. Я рассуждал так: Фиксируем $t\in S$. Далее, ясно что $x\in C_0(\mathbb{R};R)\Rightarrow \exists m\in R:x=mt+\mathrm{Im}\ \partial_1$, верно?

[alcoholist]

xmaister в сообщении #701157 писал(а):

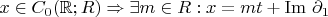
$H_0(\mathbb{R};R)$ сводится к нахождению фактора свободного модуля с множеством образующих $S$ по подмодулю, состоящего из элементов вида $M=\left\{\sum\limits_{i=1}^{k}m_i(t_i-t_i')|t_i,t_i'\in S,m_i\in R\right\}$. Получается, что $H_0(\mathbb{R},R)\cong R$. Я рассуждал так: Фиксируем $t\in S$. Далее, ясно что $x\in C_0(\mathbb{R};R)\Rightarrow \exists m\in R:x=mt+\mathrm{Im}\ \partial_1$, верно?

Группа $B_0(\mathbb{R},R)$ порождена элементами $\{r[a]-r[b]\}$ ($r\in R$), в силу тривиальности границы нульмерного сингулярного симплекса имеем $Z_0(\mathbb{R},R)=C_0(\mathbb{R},R)$.

$\forall\, c=\sum r_i[x_i]$ имеем $\sum r_i[x_i]=[0]\sum{r_i}+\sum r_i([x_i]-[0])=[0]\sum{r_i}\mod R$, поэтому гомологические классы -- это в точности элементы самого кольца (отображение факторизации $f:C_0(\mathbb{R},R)\to H_0(\mathbb{R},R)$ -- аугментация: $f(\sum r_i[x_i])=[0]\sum r_i$)