Сингулярные гомологии. Насколько я знаю, сингулярные гомологии для симплициальных комплексов и симплициальные гомологии эквивалентны. Только вот не понимаю, что мешает конструкцию, что в первом сообщении распространить на сферу?
Тут есть два варианта.
1) Если мы изображаем симплексы плоскими треугольниками. Очевидно, сфера неплоская.
2) Если мы изображаем симплексы как-угодно-гнутыми треугольниками. Тогда ничего не мешает. Но. Покрыв сферу треугольными лоскутами, мы можем это сделать только с одной заданной сферой - а не с произвольной сферой в
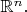
Как в такой абстрактной алгебраической конструкций можно усмотреть какую-то геометрическую информацию?
Для этого надо прорешать кучу задач на тему "вот дана такая-то геометрическая фигня, посчитать её гомологии". Для диска, сферы, тора, ленты Мёбиуса, бутылки Лейдена и т. п.
Потом обнаружить, что вообще-то этой алгебраической конструкции геометрическая "подложка" и не нужна.
И все же, зачем нужна гомология пары?
Я так понимаю - для построения точной последовательности таких гомологий. Что, неожиданно, оказывается интересной вещью и само по себе.
Я не понимаю смысла, за исключением формального представления.
Представьте себе, что вы разрезали пространство на две части. Одну из них вы назвали подпространством. Теперь вы рассматриваете не только циклы, замкнутые в колечко сами по себе (абсолютные циклы), но и циклы, уходящие "концами" в это подпространство (относительные циклы). В надежде, что они там замкнуты. А те циклы, которые целиком лежат в подпространстве, для вас гомологичны нулю.