закон распределения элемента выборки

[AndreyL]

Друзья, чего то запутался. Есть случайная величина, подчиняющаяся нормальному распределению. Берем из этой случайной величины выборку объема $n$, оцениваем по этой выборке среднее $m$ и стандартное отклонение $s$. Какому распределению подчиняется случайная величина $y=\frac{x-m}{s}$, если $x$ взят из той же выборки, по которой мы оценивали среднее и стандартное отклонение?

[AndreyL]

Пока понятно только, что при $n=2$ этот $y=\frac{x-m}{s}$ может принимать только значения или $-\frac{1}{\sqrt{2}}$ или $\frac{1}{\sqrt{2}}$, т.е. величина $\frac{y}{\sqrt{2}}+\frac{1}{2}$ подчиняется распределению Бернулли. При $n>2$ величина $y$ ограничена $-\frac{n-1}{\sqrt{n}}<y<\frac{n-1}{\sqrt{n}}$.
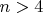
Численные эксперименты показали, что при $n=3$ распределение бимодальное с модами на границах диапазона, а при $n=4$ распределение равномерное. Далее при увеличении $n>4$ распределение становится унимодальным и медленно начинает приближаться к нормальному. Какое же это, все-таки, распределение?

[Евгений Машеров]

Скорее всего такого распределения нет, в смысле не поименовано и не изучено. Если оно имеет практическое значение - можете стать первопроходцем.
А стремиться оно, скорее всего, будет к Стьюденту (в смысле к нормальному тоже, поскольку Стьюдент стремится к нормальному, но при не очень больших n Стьюдент должен быть близок к искомому).

[AndreyL]

Понятно, спасибо! Первопроходцем в этой области быть не очень хочу - меня интересует исключительно прикладной аспект, придется просто Монте-Карлой.

[AndreyL]

AndreyL в сообщении #538037 писал(а):

При $n>2$ величина $y$ ограничена $-\frac{n-1}{\sqrt{n}}<y<\frac{n-1}{\sqrt{n}}$.

Кстати! А можно ли точно (аналитически) найти границы, которыми эта величина ограничена? Честно говоря эти границы $-\frac{n-1}{\sqrt{n}}<y<\frac{n-1}{\sqrt{n}}$ я нашел исключительно Монте-Карлой и для малых выборок. Для больших выборок диапазон, похоже, немного поуже, но это опять-же только на основании статистических испытаний. По идее границы диапазона не должны зависеть от закона распределения, которому подчиняются элементы выборки. А вот как их точно найти? Не подбором, а аналитически?

[AndreyL]

В общем получилось так: плотность распределения нормализованного элемента выборки $f(y)=g(n) \left(\frac{(n-1)^2}{n}-y^2 \right) ^{\frac{n-4}{2}}$, где $g(n)$ - множитель, обеспечивающий равенство единице интеграла плотности распределения на промежутке $-\frac{n-1}{\sqrt{n}}<y<\frac{n-1}{\sqrt{n}}$

[Toucan]

Тема перемещена из форума «Математика (общие вопросы)» в форум «Помогите решить / разобраться (М)»

[AndreyL]

AndreyL в сообщении #698121 писал(а):

В общем получилось так: плотность распределения нормализованного элемента выборки $f(y)=g(n) \left(\frac{(n-1)^2}{n}-y^2 \right) ^{\frac{n-4}{2}}$, где $g(n)$ - множитель, обеспечивающий равенство единице интеграла плотности распределения на промежутке $-\frac{n-1}{\sqrt{n}}<y<\frac{n-1}{\sqrt{n}}$

Проверил Монте-Карлой для разных объемов выборки раз сто - гипотеза о распределении принимается на уровне значимости не хуже 30%, для каждой реализации использовалось 8 тестов (Anderson-Darling, Cramér-von Mises, Jarque-Bera ALM, Kolmogorov-Smirnov, Kuiper, Pearson $\chi^2$, Shapiro-Wilk, Watson $U^2$).
Еще попробовал воспроизвести таблицу квантилей теста Граббса (таблицу квантилей взял в ГОСТ Р ИСО 5725-2-2002) - для 5%-ного квантиля ошибка в третьем знаке после запятой, для 1%-ного квантиля ошибка в четвертом знаке. Тогда получается, что таблицы больше не нужны. Также и нет смысла насчитывать таблицы для двух и более выбросов (как, например, в стандарте и здесь http://ami.nstu.ru/~headrd/seminar/publ ... zm_T_6.htm). Или я слишком самонадеян?

[AndreyL]

AndreyL в сообщении #698265 писал(а):

для каждой реализации использовалось 8 тестов (Anderson-Darling, Cramér-von Mises, Jarque-Bera ALM, Kolmogorov-Smirnov, Kuiper, Pearson $\chi^2$, Shapiro-Wilk, Watson $U^2$).

Про тесты Jarque-Bera ALM и Shapiro-Wilk я наврал, всего по 6 тестов на каждую реализацию. Больше всего на равномерное распределение похож тест $\chi^2$ Пирсона, все остальные в той или иной мере завышают уровень значимости (по результатам 588 экспериментов по 6 для каждого объема выборки от 3 до 100).