Кажись придумал. Давайте попробуем доказать необходимость по-честному (напомню, что доказал я достаточность).
Я буду писать подряд, что приходит в голову, с надеждой, что из этого получится решение. Поэтому заранее извиняюсь за беспорядок.
Итак, пусть

,

, то есть

.
Вспомним, что группа

циклическая. Пусть

,
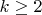
,

нечетно. Тогда

. Будем теперь считать циклы в последнем. Пусть

и

. Рассмотрим цикл

Его длина равна НОК длин циклов

и

. Посмотрим на длину

первого.
Несложно доказать, что

Пусть

,

. Имеем

. Отсюда

. Таких


штук и каждое из них входит в цикл длины

. То есть таких циклов четное количество, и они не влияют на четность перестановки.
Поэтому остались варианты:

. Сейчас мы докажем, что с ними нечетное количество четных циклов. С первыми двумя все просто: цикл

спариваем с циклом

и общее количество четное (NB в терминах

это именно то самое спаривание цикла с противоположным).
Теперь пусть

содержится в четном цикле

. Ему соответствуют два цикла с

:

и

То есть общее количество таких циклов будет четное.
Если же

-- нечетное, и

, то
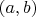
входит в четный цикл (просто потому, что цикл

четный). Но количество нечетных циклов на

нечетно, ведь

нечетно! И каждому из них соответствует ровно один цикл с

. Значит, получается нечетное количество четных циклов. Поскольку до этого у нас было четное количество четных циклов, то общее количество нечетно, что и требовалось доказать.
Фух.
-- Пт дек 07, 2012 02:28:53 --Кстати, в необходимости мы простоту

полностью не использовали, только цикличность группы.
В достаточности она действительно нужна, потому что мы там на что-то сокращаем. (Хотя, может быть, можно как-то так же, как необходимость, доказать, не используя простоту

.)