Теорема вложения соболевских в гёльдеровы

[FFFF]

Я хочу доказать, что $\forall u \in H^s(\mathbb{R}^n) \ s = \frac{n}{2}+\theta \ \theta<1 \Rightarrow u\in C^\theta(\mathbb{R}^n)$, то есть нужно сделать оценку вроде $|u(x+z)-u(x)|\leq C |z|^\theta ||u||_{H^s}$. Как доказывать для $s > \frac{n}{2}+\theta$ я знаю, при равенстве надо делать по-другому: дело свелось к доказательству ограниченности $ \forall z \in \mathbb{R}^n$ интеграла

$$\int_{\mathbb{R}^n} \frac{|e^{i z \xi}-1|^2 d\xi}{|\xi|^{2s}}$$

Похоже здесь нужно применить какой-нибудь финт из ТФКП

[Vince Diesel]

Без всяких финтов разбить область интегрирования на две: единичный шар $|\xi|\le1$ и его дополнение. Для обеих сходимость легко проверяется.

[FFFF]

Vince Diesel
С внешностью шара окей, а что делать внутри шара? Я попробовал сказать, что $|e^{i z \xi}-1|^2 \sim |z\xi|^2$, но тогда под интегралом останется $\frac{|z \xi|^2}{|\xi|^{n+2\theta}}$ у которого в нуле тоже проблемы

[ewert]

Не только зачем ТФКП, но и зачем разбивать, если этот интеграл явно считается (с точностью до постоянного множителя, который, впрочем, при желании тоже выписывается явно). Можно считать, что $z\cdot \xi=t|z|$, где $t=\xi_1$. Если теперь $x=(\xi_2,\xi_3,\ldots,\xi_n)$, то интеграл есть

$$\int\limits_{-\infty}^{+\infty}(2-2\cos t|z|)\,dt\int\limits_{{\mathbb R}^{n-1}}\dfrac{dx}{{(t^2+|x|^2)}^s}=\ldots=C\,|z|^{2s-n}=C\,|z|^{2\theta}$$

(если ничего не напутал со степенями), где постоянная

$$C=2\int\limits_{-\infty}^{+\infty}(1-\cos \tau)\cdot|\tau|^{n-1-2s}\,d\tau\cdot\int\limits_{{\mathbb R}^{n-1}}\dfrac{dy}{{(1+|y|^2)}^s}=4\int\limits_{0}^{+\infty}\dfrac{1-\cos \tau}{\tau^{2\theta+1}}\,d\tau\cdot\int\limits_{{\mathbb R}^{n-1}}\dfrac{dy}{{(1+|y|^2)}^s}.$$

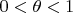
При $0<\theta<1$ этот интеграл действительно сходится.

[FFFF]

ewert
Спасибо большое, с этим всё ясно!
Получается, что такой интеграл расходится при $\theta=1$. Утверждается, что при $\theta=1$ вообще нельзя написать гёльдеровской оценки. Это можно как-то понять "на пальцах" или снова нужно оценивать интегралы?

[ewert]

FFFF в сообщении #655176 писал(а):

Утверждается, что при $\theta=1$ вообще нельзя написать гёльдеровской оценки. Это можно как-то понять "на пальцах" или снова нужно оценивать интегралы?

"Ах, ничего я не помню, и бедное сердце разбито." Вообще-то по логике вещей уж хотя бы гёльдеровость (т.е. в данном случае липшицивость) должна вроде как сохраниться (учитывая, что дальше явно должна идти по идее непрерывная дифференцируемость). Но -- не помню, а обманывать не хочу.

[FFFF]

ewert
Я не знаю, можно ли использовать как-то, что липшицевы функции почти всюду дифференцируемы, т.е. что $\frac{n}{2}+1$ соболевских "производных" недостаточно для существование одной настоящей почти всюду.

[ewert]

FFFF в сообщении #655231 писал(а):

т.е. что $\frac{n}{2}+1$ соболевских "производных" недостаточно для существование одной настоящей почти всюду.

Да, вполне возможно. Вполне возможно, что там есть зазор -- между дифференцируемостью в точном смысле и липшицевостью (допустим) по отдельным координатам. Говорю же -- не помню.