Всем привет!
Не могу решить задачу из книги Демидовича по дифференциальным уравнениям:

Ход решения довольно очевиден:
Полагаем

:

Сокращаем на x:

Или

Учитывая что

Имеем:

И после разделения переменных:
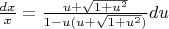
На этом этапе у меня и проблема: неопределенный интеграл функции от

. Я пробовал продифференцировать

, но это не дало никаких результатов.
Заранее спасибо.