Кстати, что это за книжку Вы читаете? Не могу определить.
Ну, давайте так. Забудем пока про представляющие функторы. Возьмем фиксированное множество

и сопоставим каждой группе

множество отображений из

в

, то есть, множество

. Это ковариантный функтор (по

): если

— гомоморфизм групп, то определено отображение

. Теперь введем на этом самом

структуру группы при помощи операции в группе

— поточечно. Тогда для гомоморфизма групп

определенное выше отображение

будет еще и гомоморфизмом групп. Это доказано выкладкой в книжке. Значит, сопоставление группе

множества

можно рассматривать как функтор не просто в категорию множеств, а в категорию групп (то есть, функтор

пропускается через забывающий функтор из категории групп в категорию множеств). Мы получили функтор из категории групп в категорию групп. Оказывается, этот функтор является представимым! То есть, есть такая замечательная группа

, что

(здесь в левой части стоит
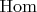
в категории множеств, а в правой — в категории групп; равенство писать не очень хорошо, нужно писать изоморфизм и помнить, что это еще означает согласованность с отображениями, которые получаются по гомоморфизмам групп

). Эта замечательная группа

называется свободной группой, порожденной множеством

, и ее построение по множеству

тоже функториально, то есть

— функтор из категории множеств в категорию групп (тот самый, про необходимость определения которого Вы говорите выше). Все это вместе означает, что функтор

является левым сопряженным к забывающему функтору

; а проще говоря — функтор

оказался представимым. Я не знаю, что написано в книжке вокруг того, что Вы процитировали, но, видимо, там это прописано недостаточно отчетливо.