Наверно можно же найти два числа (каким нибудь способом) таких, чтобы разность их произведения на 19 и 17 равна была единице?
Могу предложить свой "доморощенный" способ (не знаю, дает ли он
все решения), который заключается в том, чтобы при рассмотрении выражения

оттолкнуться от выражения

.
Далее последнее выражение немного изменяю

и получаю

;
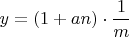
(

- целые числа)