Довольно легко найти математическое ожидание максимума из

независимых случайных величин, равномерно распределённых на отрезке
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
. Оно равно
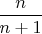
.
Нет ли где аналогичной, можно оценочной, формулы для матожидания максимума из

независимых случайных величин, нормально распределённых с одинаковым матожиданием и дисперсией?
Матожидание максимума из

независимых случайных величин, распределённых по одинаковому закону имеет вид
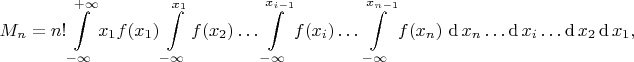
где

— плотность вероятности распределения. Пусть
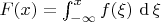
— соответствующая функция распределения, тогда имеем
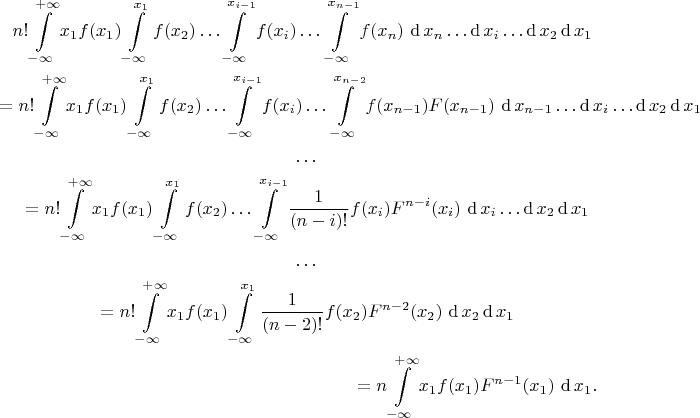
Таким образом
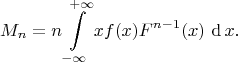
Можно убедится, что для равномерного распределения полученная формула дает выражение, приведенное в процитированном сообщении.
Подставив в полученную формулу плотность вероятности и функцию распределения нормального распределения с матожиданием

и дисперсией

![\begin{equation*}
f(x)
=
\dfrac{1}{\sigma\sqrt{2\pi}}
\exp\left[-\dfrac{1}{2}\left(\dfrac{x-a}{\sigma}\right)^2\right]
,\quad
F(x)
=
\frac{1}{2}
+
\frac{1}{2}
\mathop\mathrm{erf}\left(\dfrac{x-a}{\sqrt2\sigma}\right)
,
\end{equation*} \begin{equation*}
f(x)
=
\dfrac{1}{\sigma\sqrt{2\pi}}
\exp\left[-\dfrac{1}{2}\left(\dfrac{x-a}{\sigma}\right)^2\right]
,\quad
F(x)
=
\frac{1}{2}
+
\frac{1}{2}
\mathop\mathrm{erf}\left(\dfrac{x-a}{\sqrt2\sigma}\right)
,
\end{equation*}](https://dxdy-04.korotkov.co.uk/f/b/d/5/bd5d320df718dc091a3bdcba4695e73f82.png)
получим
![\begin{equation*}
M_n
=
n
\int\limits_{-\infty}^{+\infty}
x
\dfrac{1}{\sigma\sqrt{2\pi}}
\exp\left[-\dfrac{1}{2}\left(\dfrac{x-a}{\sigma}\right)^2\right]
\left[
\frac{1}{2}
+
\frac{1}{2}
\mathop\mathrm{erf}\left(\dfrac{x-a}{\sqrt2\sigma}\right)
\right]^{n-1}
\,\mathop{\mathrm{d{}}} x
.
\end{equation*} \begin{equation*}
M_n
=
n
\int\limits_{-\infty}^{+\infty}
x
\dfrac{1}{\sigma\sqrt{2\pi}}
\exp\left[-\dfrac{1}{2}\left(\dfrac{x-a}{\sigma}\right)^2\right]
\left[
\frac{1}{2}
+
\frac{1}{2}
\mathop\mathrm{erf}\left(\dfrac{x-a}{\sqrt2\sigma}\right)
\right]^{n-1}
\,\mathop{\mathrm{d{}}} x
.
\end{equation*}](https://dxdy-04.korotkov.co.uk/f/b/b/b/bbbe4a1efb5572f92eb3f260c61ec65e82.png)
Произведя замену переменных
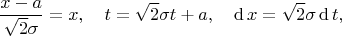
получим
![\begin{multline*}
M_n
=
\dfrac{\sigma n}{\sqrt{2\pi} 2^{n-2}}
\int\limits_{-\infty}^{+\infty}
t\exp\left(-t^2\right)
\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^{n-1}
\,\mathop{\mathrm{d{}}} t
\\
+
\dfrac{a n}{\sqrt{\pi} 2^{n-1}}
\int\limits_{-\infty}^{+\infty}
\exp\left(-t^2\right)
\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^{n-1}
\,\mathop{\mathrm{d{}}} t
.
\end{multline*} \begin{multline*}
M_n
=
\dfrac{\sigma n}{\sqrt{2\pi} 2^{n-2}}
\int\limits_{-\infty}^{+\infty}
t\exp\left(-t^2\right)
\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^{n-1}
\,\mathop{\mathrm{d{}}} t
\\
+
\dfrac{a n}{\sqrt{\pi} 2^{n-1}}
\int\limits_{-\infty}^{+\infty}
\exp\left(-t^2\right)
\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^{n-1}
\,\mathop{\mathrm{d{}}} t
.
\end{multline*}](https://dxdy-03.korotkov.co.uk/f/2/2/9/229003bcd64b71a6f270ff2880a843ea82.png)
Вычисления дают
![\begin{equation*}
\int\limits_{-\infty}^{+\infty}
\exp\left(-t^2\right)
\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^{n-1}
\,\mathop{\mathrm{d{}}} t
=
\left.
\dfrac{\sqrt\pi}{2}
\dfrac{\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^n}{n}
\right|_{-\infty}^{+\infty}
=
\dfrac{\sqrt\pi 2^{n-1}}{n}
.
\end{equation*} \begin{equation*}
\int\limits_{-\infty}^{+\infty}
\exp\left(-t^2\right)
\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^{n-1}
\,\mathop{\mathrm{d{}}} t
=
\left.
\dfrac{\sqrt\pi}{2}
\dfrac{\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^n}{n}
\right|_{-\infty}^{+\infty}
=
\dfrac{\sqrt\pi 2^{n-1}}{n}
.
\end{equation*}](https://dxdy-04.korotkov.co.uk/f/3/5/8/358abc60f0749b7ba1f4a84f78f6cacc82.png)
Осталось вычислить (или оценить) интеграл
![\begin{equation*}
\int\limits_{-\infty}^{+\infty}
t\exp\left(-t^2\right)
\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^{n-1}
\,\mathop{\mathrm{d{}}} t
.
\end{equation*} \begin{equation*}
\int\limits_{-\infty}^{+\infty}
t\exp\left(-t^2\right)
\left[1 + \mathop\mathrm{erf}\left(t\right)\right]^{n-1}
\,\mathop{\mathrm{d{}}} t
.
\end{equation*}](https://dxdy-01.korotkov.co.uk/f/4/8/8/488aff563907902479d949376069271b82.png)