Восемь точек на плоскости

[Nikolai Moskvitin]

Продолжаю решать открытые математические проблемы. Вот ещё одна идея (как всегда, я останавливаюсь там, где начинается теория чисел).

Можно ли разместить 8 точек на плоскости так, чтобы никакие три из них не лежали на одной прямой, никакие четыре не лежали на одной окружности и расстояние между любыми двумя точками было целым числом?

Идея: берутся четыре точки, для которых это верно (существует же четырёхугольник с целыми сторонами и диагоналями). Пусть они образуют вершины параллелограмма (тут надо доказать, что такое возможно, а если нет, взять общий случай четырёхугольника- но тогда может не получиться) . Теперь, "сохранив копию", переносим параллелограмм параллельным переносом на расстояние, являющееся целым числом, в направлении, не перпендикулярном ни одной прямой, содержащей сторону параллелограмма; при этом это направление не должно также совпадать с направлением ни одной из сторон и ни одной из диагоналей (тогда параллелограммы, очевидно, не вписаны в окружность, и никакие три точки не лежат на одной прямой). Так как расстоние параллельного переноса одно и то же, согласно формулам, связанным с параллелограммом, получаем: $2a^2+2b^2=c^2+d^2 $; где $a$ - длина противолежащих сторон первоначального параллелограмма,$ b$-расстояние, на которое он переносится параллельным переносом, $c$,$ d$, - диагонали параллелограммов, образованных
этими сторонами, параллельными им отрезками и отрезками длиной b. Эту же формулу надо применить и для других параллелограммов.

Рассмотрите эту конструкцию-наверняка она может быть решением.
Если два этих параллелограмма- $ABCD$ и $A'B'C'D'$, и у них соблюдены все указанные условия, то надо определить, могут ли диагонали всех параллелограммов ($AB'$, $A'B$, $BC'$, $B'C$,$ DC'$, $D'C$, $DB'$, $AC'$) быть целыми числами одновременно . Вопрос о прямых и окружностях применительно к этой конструкции тогда можно опустить.

С уважением, Николай.

[Nikolai Moskvitin]

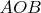
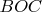
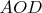
Ещё более красивая идея (на случай, если та не пройдёт; может, и эта не пройдёт...). Взять параллелограмм $ABCD$, у коготорого стороны и диагонали целые, а угол между диагоналями равен $\frac{\pi}{6}$ Отметить точку их пересечения O. Затем отметить центры описанных окружностей треугольников $AOB$, $BOC$, $COD$, $AOD$ как $O_1$,$O_2$,$O_3$,$O_4$.

У меня уже есть два доказанных ранее утверждения, рассмотрение частных случаев которых приводит к двум леммам, будет и третья.

Утверждение 1.

Условие: в четырёхугольнике $ABCD$ проведены диагонали $AC$ и $BD$, пересекающиеся в точке $O$; для каждого из образовавшихся треугольников отмечен центр описанной окружности.

Доказать: эти центры являются вершинами параллелограмма.

Утверждение 2.
Условие: в треугольнике $ABC$ проведена чевиана $BD$, образующая со стороной $AC$ угол $ b$. Расстояние между центрами описанных окружностей треугольников $ABD$ и $BDC$ равно $a$.

Доказать: $AC=2a\sin{b}$

Доказательство первого утверждения.

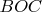
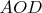
Решение: пусть $O_1$,$O_2$,$O_3$,$O_4$- центры описанных окружностей треугольников соотвественно $ABO$, $BOC$, $COD$ и $AOD$. $BO_2=O_2O$ и $BO_1=OO_1$, следовательно, $BO$ перпендикулярен $O_1O_2$, Аналогично, $O_3O_4$ перпендикулярен $OD$. Но $B$, $O$, $D$ лежат на одной прямой, следовательно, $O_1O_2$ параллелен $O_3O_4$. Аналогично, $O_2O_3 $параллелен $O_1O_4$.

Доказательство второго утверждения.

Решение: треугольник $ DO_1O_2$ подобен треугольнику $ABC$, так как, очевидно, $\angle{DO_2O_1}=\angle{DCB}$ и $\angle{O_1DO_2}=\angle{ABC} $. Тогда $AB=2R\sin{b}$,$\frac{R}{AB}=\frac{O_1O_2}{AC}$, отсюда $ 2R\sin{b}=\frac{R(AC)}{O_1O_2}$, отсюда выводится искомая формула.

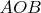
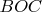
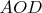
Исходя из этих утверждений, можно определить, что четырёхугольник $O_1O_2O_3O_4$ нельзя вписать в окружность и что его стороны равны диагоналям параллелограмма $ABCD$ (того, что упоминался в начале). Радиусы окружностей, описанных около треугольников $AOB$, $BOC$, $COD$, $AOD$ по усиленной теореме синусов, уже применявшейся для доказательства второго утверждения, будут целыми и и будут равны сторонам $ABCD$. (например, $\frac{AB}{\sin{AOB}}=2R$...).
Заметим, что, так как треугольники, на которые разбивает точка пересечения диагоналей данный параллелограмм, не равнобедренные, то $C$, $O_2$, $O_1$ не лежат на одной прямой. Ясно, что других троек точек, лежащих на одной прямой, тоже- в данной конструкции- не существует. Далее, $A$, $O_1$, $O_2$, $C$ не лежат на одной окружности, так как $O_1O_2=AC$ и $CO_2$ не параллелен $AO_1$ ($O_1$ находится вне треугольника $ABC$, а $O_2$ внутри). Также $O_1O_2$ не параллелен $AC$, ибо $O_1O_2$ перпендикулярен $AB$, а $AC$ не перпендикулярен. $O_1BCO_2$ не может быть вписан в окружность, поскольку противолежащие углы $BO_1O_2$ и $BCO_2$-острые. Применяя подобные рассуждения, можно, как и в прошлый раз, сказать, что осталось только проверить существование целых отрезков, соответствующих задаче. С помощью теоремы косинусов и формулы для параллелограмма можно вывести ряд условий: $2a^2+2b^2=c^2+d^2$ (1), где$ a$ и $ b$, $c$ и $d$- соотвественно стороны и диагонали рассматриваемого параллелограмма.$ a^2+b^2-ab=m$, $a^2+b^2+ab=n$. Последний штрих, вносящий сомнение в применимости конструкции: я забыл о целочисленности отреков $CO_1$, $AO_2$... и т.д. Так как $AO_1=AB$, а $\angle {O_1AO}=\frac{\pi}{2}-\angle{ABD}$ и при этом $\cos\angle {ABD}$- число рациональное, то получаем, что если $\sin\angle{ABD}$ также рационален, есть всё-таки надежда...хотя уже слабая.

С уважением, Николай.

ps Добавил минут через двадцать: можно рассмотреть не параллелограмм, а произвольный четырёхугольник, лишь бы его стороны и диагонали были целыми числами, а угол между диагоналями был равен $\frac{\pi}{6}$. Но всё равно надежда слабая.

[Nikolai Moskvitin]

У меня проблема: система не отображает знак корня совсем. Поэтому написал специально неправильно и прошу администратора поправить.

Пусть надо найти четырёхугольник $ABCD$ с целыми сторонами, диагоналями и углом между ними$ \frac{\pi}{6}$.
Пусть точка пересечения диагоналей- O. Обозначим стороны $AB=a$, $BC=b$, $CD=с$, $BC=d$, диагонали $BD=e$, $AC=f$, отрезки $AO=x$, $BO=y$.
Получается система:
$x^2+y^2-xy\sqrt3=a^2 $(1),
$x^2+(e-y)^2+x(e-y)\sqrt3=b^2$ (2),
$(e-y)^2+(f-x)^2-(e-y)(f-x)\sqrt3=c^2 $(3),
$y^2+(f-x)^2+y(f-x)\sqrt3=d^2 $(4)

Вычитаем (3) из (2): $x^2-(f-x)^2+x(e-y)\sqrt {3}+(e-y)(f-x)\sqrt {3}=b^2-c^2$(5) После преобразований приходим к уравнению:
$f(2x-f)+(e-y)f \sqrt{3}=b^2-c^2$. (6) Возьмём параметр $\alpha$, такой, что$ y=\alpha\sqrt {3}$ Преобразуем уравнение (6): $f(2x-f+(e-y)\sqrt {3})=m$, где$ m=b^2-c^2$; $f$-целое, поэтому выражение $2x+e(\sqrt {3})$- должно быть целым. Можно выбрать такой $x$, что это действительно будет выполняться.

Комментарий: следует найти параметр $\alpha$.
С уважением, Николай

[venco]

(Оффтоп)

Nikolai Moskvitin в сообщении #612230 писал(а):

У меня проблема: система не отображает знак корня совсем.

Корень пишется через q:
\sqrt3
$\sqrt3$

[Someone]

(Оффтоп)

Про корень Вам уже написали, но добавлю: $\sqrt[n]{ABC}$ кодируется как \sqrt[n]{ABC}.
В формулах нельзя употреблять русские буквы. Точнее, можно, но в виде \text{русский текст}. Например: $A_{\text{низ}}^{\text{верх}}$ получается из $A_{\text{низ}}^{\text{верх}}$.

[scwec]

(Оффтоп)

А я подтвержу, что параллелограммы с целыми сторонами и целыми диагоналями да еще и с целыми площадями имеются в неограниченном количестве.

[Nikolai Moskvitin]

В общем, повозился немного с уравнениями и получил следующее:

Запишем: $y^2+x^2+xy \sqrt {3}=a^2$ (1)
$y^2+(f-x)^2-y(f-x) \sqrt 3=b^2$(2)
$(f-x)^2+(e-y)^2+(f-x)(e-y)\sqrt 3=c^2$(3)
$x^2+(c-y)^2-x(e-y)\sqrt 3=d^2$.(4)

Вычитаем (2) из (1) и (4) из (3) и получаем (5) и (6):

$2fx-f^2+yf\sqrt 3=a^2-b^2$(5)
$f^2-2fx+f(e-y)\sqrt 3=c^2-d^2$ (6)

Складываем (5) и (6) и получаем (7):

$ef=a^2-b^2+c^2-d^2$ (7) Если его решить, получиться решение задачи!!! Зря я так сомневался!

-- 30.08.2012, 16:34 --

Нет! Всё-таки два расстояния будут нецелыми- это, собственно говоря, $O_1O_3$ и $O_2O_4$. Даже $AO_2$-целое... Значит, это не решение... Попробуйте тогда с параллелограммами! По крайней мере, удалось доказать, что ровно $\frac{n(n-1)}{2}-2=26$ расстояний при данной конструкции могут быть целыми. Это тоже результат.

[longstreet]

Nikolai Moskvitin в сообщении #611681 писал(а):

Можно ли разместить 8 точек на плоскости так, чтобы никакие три из них не лежали на одной прямой, никакие четыре не лежали на одной окружности и расстояние между любыми двумя точками было целым числом?

Вроде это должно быть как-то связано с теорией Рамсея...

[Nikolai Moskvitin]

longstreet в сообщении #612616 писал(а):

Вроде это должно быть как-то связано с теорией Рамсея...

В Википедии пишут, что с помощью неё можно доказать существование, а конструктивно построить существующую систему она не даёт возможности. Мне лично вообще не очень нравится такой подход. Есть направление в математике, выступающее за конструктивное решение. Поэтому пока что надо проверить случай с параллелограммами.

[longstreet]

Во-первых, насколько я знаю, нельзя так обобщать.

Во-вторых, интересующий факт, а именно "можно ли?" ни чуть не хуже может быть доказан неконструктивно. Более того, неконструктивное доказательство $-$ ближе чистой математике. Вы, кажется, не понимаете следующего. Интересующая вас задача настолько просто по формулировке и реализации проверки, что можно заставить компьютер весьма эффективно перебирать варианты построений. Думаю, если это действительно открытая проблема, это делал ни один человек, а много. Однако, если такого построения не существует, то вы так и будете перебирать варианты без остановки, а можно остановиться и подумать, а разрешима ли задача вообще и математически показать, что нет. Иногда другого и выхода нет.

[Nikolai Moskvitin]

Спасибо Вам большое! А то бы я так и продолжал

longstreet в сообщении #612647 писал(а):

перебирать варианты без остановки

. Попробую хотя бы начать изучать.

[AKM]

Тема перемещена из форума «Дискуссионные темы (М)» в форум «Карантин»
по следующим причинам: много синтаксических ошибок в сообщении этом. Часть связана с использованием в формулах русской буквы О (вместо латинской O). И остальные сообщения требуют правок ("scrt").

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.

[AKM]

Тема перемещена из форума «Карантин» в форум «Помогите решить / разобраться (М)»
Причина переноса: не указана.

[Nikolai Moskvitin]

Добрый день!

Помучившись немного, получил шестнадцать условий (не считая целочисленности сторон и диагоналей четырёхугольника $ABCD$), при которых вторая конструкция работает (по поводу четырёх последних см. замечание ниже). Пусть если O- точка пересечения диагоналей, $AO=x$, $BO=y$, $AC=f$, $BD=e$, $\angle{ABO}=\alpha$, $AB=a$, $BC=b$, $CD=c$, $AD=d$, $E$ и $G$- проекции $O_1$ и $O_2$ на $AC$ соответственно. $m_n$- любые натуральные числа.
$\frac{e^2+f^2+2ef\cos\alpha}{4\sin^2\alpha}={m_1}^2$ (1);
$\frac{e^2+f^2-2ef\cos\alpha}{4\sin^2\alpha}={m_2}^2$ (2);
$fx={m_3}^2-\frac{b^2}{4\sin^2\alpha}$(3);
$f^2-fx={m_4}^2-\frac{a^2}{4\sin^2\alpha}$(4);
$ey={m_5}^2-\frac{c^2}{4\sin^2\alpha}$(5);
$e^2-ey={m_6}^2-\frac{d^2}{4\sin^2\alpha}$(6);
Аналогичные (7),(8),(9),(10)
(11) и (12)- условия рациональности чисел $ \sin\alpha$ и $\cos\alpha$
$O_1E>2O_2G$(13) и аналогичные (14),(15),(16)

Последняя группа условий доказывается через "неподобие" треугольников $AO_2G$ и $ CO_1E$ и аналогичных пар треугольников.

С уважением, Николай
ps нашёл хорошую книгу по теории Рамсея- Грэхэма.

[Алексей К.]

(Оффтоп)

Nikolai Moskvitin в сообщении #616611 писал(а):

ps нашёл хорошую книгу по теории Рамсея- Грэхэма.

По информативности последняя фраза почти эквивалентна "ps сегодня хорошо поспал".