Добрый вечер!
Читая, наткнулась на термин "погружение" (в топологии).
Посмотрела определение, но не очень его поняла:
Цитата:
В топологии, погружение — такое отображение

одного топологического пространства в другое, при котором каждая точка в

имеет окрестность

, которую
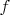
гомеоморфно отображает на

.
Наверное, мои вопросы покажутся глупыми, но я только учусь, к тому же сама.

1. Что за

?
2. Что с

?
Или

в

- как аргумент функции?
Просто пока что я представить не могу даже этого.
Объясните пожалуйста!
Спасибо.
