3 человека стреляются на дуэли, стреляют по очереди (жребий) вероятность попаданий

требуется определить стратегию каждого.
на мой взгляд

должен стрелять в воздух пока все живы...
но вот в доказательстве у меня проблема..
1 часть (пытаюсь доказать что

выгодно стрелять в воздух .
рассмотрим каждого

стреляет первым рассмотрим 3 варианта
1. Стреляет в

(попадает и

промахивается в

) либо (промах и ситуация переходит в
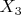
)
2. Стреляет в

(попадает и

промахивается в

) либо (промах и ситуация переходит в
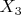
)
3. Стреляет в воздух эквивалентно ситуация
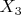


таким образом либо стреляет в

либо в воздух
аналогично


таким образом либо стреляет в

либо в воздух


таким образом либо стреляет в

либо в воздух
переходим к стратегиям вторых стрелков

перед


или


или


или


т.к.


т.к.

стратегии третьих стрелков (верхний индекс - первый стрелок)

или


или

в зависимости от стратегий


т.к

не стреляет в


т.к в

не стреляет ни кто

получаем что

может стрелять в воздух от этого вероятность выживания не ухудшиться...
-- 24.05.2012, 12:59 --часть 2
посчитаем все вероятности.
вся дуэль сводится к дуэли

и победитель дуэлиться с

при этом у

первый выстрел вне зависимости кто победит




получается в воздух им стрелять не выгодно..
рассчитаем вероятности выжить

перестрелке


аналогично

рассчитаем вероятности выживания

в перестрелке

верхний индекс показывает каким по счету стреляет



т.к очередность выбирается случайно, то

высчитываем общую вероятность выжить одному из стрелков



получил

т.е если бы он стрелял в

он бы выживал с вероятностью

получил противоречие...
не могу понять где не ошибся..