Имеется лагранжиан

- добавочная функция

Каков класс функций

, при которых уравнения Лагранжа

не изменятся?
Как пытаюсь делать:
Рассматриваю уравнения с одной обобщённой координатой:
Заменой
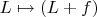
получаю
Очевидно, что можно прибавить или умножить (

) на константу. Как найти остальные случаи?