На стр. 77 уравнение (3.3) умножается на матрицу, обратную к

, т.е. на

. Почему умножают на неё слева, а не справа…
Вы просто перепутали два формализма. Когда векторы-матрицы записываются без индексов, к ним применяются понятия "умножить справа, умножить слева", они могут быть "транспонированы" и т. д. А когда записываются индексы и используется соглашение о суммировании, на всё это можно наплевать, спокойно переставлять множители местами, и просто смотреть, какой индекс с каким совпадает. То есть

но при этом

Н стр. 78 выдвигается требование к полученным уравнениям, чтобы они были совместны. Вопрос: в каком смысле? Говорится, что по своему геометрическому смыслу. Однако мне не ясно, что это вообще за геометрический смысл совместности. В чём заключается этот геом. смысл?
Здесь всего-то "геометрического смысла" - в том, что функция

задаёт соответствие целой
области плоскости

и каких-то точек в (здесь 3-мерном) пространстве
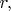
так что все функции от

определены именно как функции на какой-то области, и для них должны выполняться стандартные соотношения между частными производными. Под "нулевой кривизной", видимо, подразумевается то, что пространство
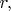
в котором лежит образ области, само по себе неискривлённое.
Но вообще, я гляжу, всё изложение сильно с другой стороны, чем привычно, скажем, физикам. Не уверен, что эту книжку стоит читать
как первую.