поверхность уровня

[svv]

bayak писал(а):

Но если $\varphi=\frac{1}{a}\arctg\frac{x_3}{x_4}$, то $d\varphi \cong x_4 dx_3-x_3 dx_4$.

Надо, наконец, разобраться с этим, иначе шансов договориться не будет.
Рассмотрим плоскость с декартовыми координатами $x, y$. Я задаю прямую параметрически:

$$\begin{cases}x=\varphi\\y=a\varphi\end{cases}$$

где $a=\operatorname{const}$. Естественно, $\varphi$ не имеет здесь смысла угла, я просто хотел сохранить обозначения.

Найдём градиент $\varphi$ в координатах $x, y$. Так как $\varphi=x$, то
$\nabla\varphi=\left(\frac{\partial \varphi}{\partial x}, \frac{\partial \varphi}{\partial y}\right)=\left(\frac{\partial x}{\partial x}, \frac{\partial x}{\partial y}\right)=(1, 0)$. Или, на языке дифференциальных форм, $d\varphi=dx$. Согласны?
Скобки у меня -- это не скалярное произведение, а перечисление компонент.

Очень хорошо. Сейчас я докажу, что всё это неправильно. Так как $\varphi=\frac y a$, имеем:
$\nabla\varphi=\nabla\frac y a = \frac 1 a \left(\frac{\partial y}{\partial x}, \frac{\partial y}{\partial y}\right)=\frac 1 a (0, 1)$. Или на языке форм:
$d\varphi=d\left(\frac y a\right)=\frac 1 a dy$.

В чём ошибка?
Так как никто не убедит человека лучше, чем он сам, пожалуйста, сформулируйте мою ошибку в этом учебном примере своими словами.

[bayak]

svv в сообщении #542659 писал(а):

В чём ошибка?
Так как никто не убедит человека лучше, чем он сам, пожалуйста, сформулируйте мою ошибку в этом учебном примере своими словами.

Ошибка в том, что $\varphi$ параметрическая координата, а нам (мне) надо её превратить в функцию, градиент которой в точках координатной линии равен касательным векторам. Поэтому правильно будет так:

$$d\varphi=\frac{dx(\varphi)}{d\varphi}dx+\frac{dy(\varphi)}{d\varphi}dy=dx+ady,$$

где слева от знака равенства $\varphi$ это искомая функция, а справа от равенства все $\varphi$ всё ещё параметрические координаты.

[svv]

bayak писал(а):

$$d\varphi=\frac{dx(\varphi)}{d\varphi}dx+\frac{dy(\varphi)}{d\varphi}dy=dx+ady,$$

Нет, bayak, простите, не договоримся. Слишком разные подходы. Может, кто-нибудь другой Вас поймёт.

[bayak]

svv в сообщении #542893 писал(а):

Нет, bayak, простите, не договоримся. Слишком разные подходы. Может, кто-нибудь другой Вас поймёт.

Может быть у нас и разные подходы, но Вы мне уже помогли и могли бы помочь ещё. Поэтому я благодарен Вам сейчас и буду багодарен в будущем.

[svv]

Спасибо и Вам. Ну, конечно, в будущем могут быть более взаимопонимаемые темы.

[bayak]

svv в сообщении #542893 писал(а):

bayak писал(а):

$$d\varphi=\frac{dx(\varphi)}{d\varphi}dx+\frac{dy(\varphi)}{d\varphi}dy=dx+ady,$$

Нет, bayak, простите, не договоримся. Слишком разные подходы. Может, кто-нибудь другой Вас поймёт.

Собственно, а что Вас смутило? Если бы я написал:

$$df=\frac{dx(\varphi)}{d\varphi}dx+\frac{dy(\varphi)}{d\varphi}dy=dx+ady,$$

где $\frac{dx(\varphi)}{d\varphi}=\partial_{x}f$, $\frac{dy(\varphi)}{d\varphi}=\partial_{y}f$, то мы бы договорились? А может быть смущает то, что в этой формуле неявно предполагается заданным семейство параллельных параметризованных прямых?

[svv]

Пусть, например, $a=1$, тогда кривая будет $y=x$.
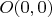
Возьмём на ней две точки: $O(0,0)$ и $A(1,1)$. Ясно, что они получаются при значениях $\varphi$ соответственно $0$ и $1$.
По моим представлениям, $d\varphi=dx$ -- это правильный вариант. Проверим его так. Найдём изменение $\varphi$ от точки $O$ до точки $A$. Так как изменение $x$ равно $1$, то и изменение $\varphi$ равно $1$. Всё правильно.
Теперь посчитаем по Вашей формуле $d\varphi=dx+dy$, получаем, естественно, $2$. Приходится формулу забраковать как ошибочную.

bayak писал(а):

Ошибка в том, что $\varphi$ параметрическая координата, а нам (мне) надо её превратить в функцию, градиент которой в точках координатной линии равен касательным векторам.

Так... Я так понял, что Вы все координаты $\rho, \theta, \varphi$ рассматриваете сначала только на поверхности, правильно? Потом Вы хотите, если я правильно понял, распространить их на всё пространство -- с соблюдением указанного условия (на градиент). Ну, а почему нельзя сразу считать их заданными в $\mathbb R^4$? Ведь Ваши уравнения очень располагают к этому.

Боюсь сразу задавать все вопросы. Хочу добиться консенсуса в простом вопросе: как мы оба понимаем градиент. Если я вычисляю градиент $\rho, \theta, \varphi$ как функций, заданных во всем пространстве (а не только на поверхности), то, по моим представлениям, я не имею права пользоваться такими уравнениями, в которые входит $a$, так как это привязывает изменение координат $\rho, \theta, \varphi$ к поверхности и тем самым искажает (а лучше сказать: калечит) градиент.

Поэтому уравнением $\varphi=\arctg\frac{x_1}{x_2}$ я пользоваться могу -- оно выполняется во всем пространстве, а уравнением $\varphi=\frac{1}{a}\arctg\frac{x_3}{x_4}$ нет, оно выполняется только на поверхности (если считать $a$ константой, а можно и не считать), и вычисленный с её помощью градиент $\varphi$ -- это будет непонятно что.

[bayak]

svv в сообщении #543046 писал(а):

Приходится формулу забраковать как ошибочную.

Да нет же, просто в этой формуле $\varphi$ уже не параметрическая координата прямой, а производная от неё функция на плоскости (выше я писал об этом и даже предложил назвать её буквой f).

Давайте возьмём ещё один простой пример. Пусть дана параметрическая окружность:

$$\begin{cases}x=\cos\varphi\\y=\sin\varphi\end{cases},$$

а требуется найти соответствующую ей поверхность уровня. Поскольку $x'=\cos'\varphi=\sin\varphi=y$, $y'=\sin'\varphi=-\cos\varphi=-x$, то в моей интерпретации достаточно получить дифференциальную форму $d\varphi=ydx-xdy$, откуда мы легко найдем ортогональную ей форму $df=xdx+ydy$ и получим поверхность уровня $f=x^{2}+y^{2}=1$, совпадающую с параметрической окружностью. С другой стороны, поскольку $\frac{x}{y}=\ctg\varphi$, то $\ctg\varphi=\frac{x}{y}$, следовательно $\varphi$ можно интерпретировать как функцию на плоскости, а не как параметр на окружности. Тогда мы имеем форму $d\varphi \cong ydx-xdy$ и ортогональную ей форму $df\cong xdx+ydy$. Наверно, можно найти и соответствующую поверхность уровня. Надеюсь пока мы друг друга понимаем.