Допустим, что существует. Пусть

. Тогда

и

при

. Если бы для какого-либо

было

, то тогда

(вследствие

) и
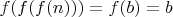
, а значит

- противоречие. Поэтому

при всех

. В частности,

. Учитывая, что

, получаем, что

. Но тогда, учитывая вышесказанное,

и

, стало быть,

- противоречие.
