alcoholist, не путайте ТС, пожалуйста, тем более в его задании нужно найти проекцию точки М0 на прямую, а не только расстояние
т.М0 до прямой.
Andrei94, пред вами компьютр - неужели тяжело посчитать расстояние между двумя точками?
А я посчитал на компьютере
http://www.wolframalpha.com/input/?i=sq ... %29%5E2%29-- 29.11.2011, 15:51 --А почему так сложно решали?
Ведь параметрическое уравнение прямой можно сразу написать:

.
Расстояние от точки до ее проекции -- по учебнику:

а саму проекцию

(это точка на прямой) находим из соотношения ортогональности

А что такое
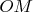
?
(Оффтоп)
пока что соотношения в векторной форму трудновато воспринимаются мной...
Andrei94, вы и там ухитрились сделать ошибку.Честно говоря, вы меня утомили своей небрежностью.
-- Вт ноя 29, 2011 17:29:05 --alcoholist, ну что вы его путаете, он не может без ошибок в Вольфраме записать.Пусть доделает до конца, тем методом который начал.