Я тут картинку нарисовал. На первом фрагменте зелёненькая фиксированнаая прямая, она совпадает с осью ординат. Синяя окружность как бы движется. Обе линии ориентированы. И есть угол

пересечения между ними, иногда мнимый, типа

, иногда комплексный, вроде

. График цвета фуксии (прямая) — зависимость

, где

— положение центра движущейся окружности. И этот косинус бывает 4, и даже больше.

А на втором фрагменте я подменил зелёную прямую зелёной окружностью, тоже фиксированной. Ну, график в параболу превратился.
[updated 18.11]
Картину подправил. Для окружности

(касание), для
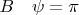
("антикасание").