Насколько я понял, дело обстоит так. Каждая гиперповерхность из
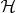
почти однозначно определяется парой
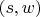
; "почти" в том смысле, что
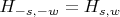
. Если бы этого "почти" не было, то можно было бы считать, что
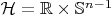
. Чтобы получить правильное равенство, мы рассматриваем действие группы
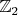
на
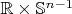
:
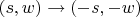
.
Тогда требуемое равенство
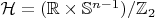
означает что
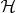
равно (или изоморфно, или биективно) множеству орбит этого действия.
---------------------------------------------
Извините, забыл добавить: если группа

действует на множестве

, то через
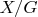
часто обозначают множество орбит этого действия (что здесь и делается).