Давайте тогда формулу метрики в этой горловине при

. Для сравнения с Райсснером-Нордстрёмом.
Для внутреннего мира электрического заряда в метрике

есть решение уравнений Эйнштейна и Максвелла (

) :
(1)


где

и
-
плотности энергии электромагнитного поля и пыли соответственно,

,

.
1) При

метрика переходит в метрику Толмана [ЛЛ2].
2) При

метрика переходит в метрику Рейсснера-Нордстрема [МТУ].
3) При

- в метрику Шварцшильда [ЛЛ2].
Из-за того, что

, радиус гауссовой кривизны радиальных сфер

никогда и нигде не обращается в ноль, - вот в чём вся "соль" этого, казалось бы, слегка отличного от общеизвестных, решения уравнений ОТО. К чему это привело? Коллапса в центр нет. Основной сингулярности
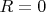
нет. Черной дыры нет. Горизонтов типа шварцшильдовского нет. Что появилось нового? При

(

- один из первых интегралов уравнений Эйнштейна, задаваемый, совместно с двумя другими - зарядом

и гравитационным радиусом

(полной гравитационной энергией внутреннего мира на данном радиусе

) произвольно, т.е. какими-то начальными условиями ) возник нестационарный периодический во времени мир из незаряженной пыли, пульсирующий от состояния максимального сжатия до состояния максимального расширения (вселенная), но - снабженный двумя статическими сферами экстремальной кривизны (горловинами, horns) с радиусом, в точности равным обычно используемому в физике элементарных частиц т.н. "классическому радиусу"

,
где

- полная (гравитационная) энергия этого нестационарного мира (вселенной) на горловинах, геометрически описываемая т.н. гравитационным радиусом

.
Все геометрические и физические величины на этих горловинах - конечны и постоянны. Из-за большого "гравитационного дефекта массы", т.е. фокусирующего (притягивающего) действия гравитационного поля (т.е. из-за сильной кривизны пространства) масса на горловинах, как и их радиус, могут быть намного меньше, чем параметры внутреннего мира, т.е. эти горловины по сути являются элементарными частицами (классическими, естественно).
Затем можно разрезать внутренний мир по горловине и склеить его с вакуумным статическим миром, в результате чего получается взгляд на заряд как бы "со стороны" : его "обнаженная" горловина выглядит как покоящаяся элементарная частица (классическая, в данном представлении).
Статическая экстремальная поверхность определяется условием :

.
Отсюда из (1) следует :

,
где

- классический (электромагнитный ) радиус.