Ряды прекрасны...
Я чего-то подумал, что может быть надо найти ряд

, сходящийся только при

, где

непрерывная функция? Тогда это может быть интересно.
Ну так не бывает, потому что тогда должно быть

при

и

при

, то есть

и

при всех

, что противоречит непрерывности.
Здравствуйте, участники форума. Только начали в ВУЗе ряды проходить. Многим известно, что ряд
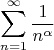
сходится при

> 1 и расходится при

1. Нам сказали подумать насчет того, что найти пример ряда

, который бы сходился при

1 и расходился при

> 1. Или доказать, что таких рядов не существует...
Ну, например,

или

или... мало ли чего еще придумать можно;)