Сомневаюсь в решении.
Задача 1. Какова размерность пространства вещественных квадратных матриц порядка

с нулевым следом?
Такая матрица
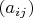
определяется всеми элементами кроме одного на диагонали (пусть
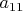
), который подбирается, чтобы сделать след нулевым. Базисом будут матрицы
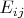
,

кроме

; их

.
Задача 2. Какова размерность пространства всех многочленов

степени

от одной переменной с условием
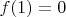
?
Аналогично получил

(подбираем один коэффициент).