Спасибо.

В принципе, я сам это доказал - и счас увидел, что мне ответили. Спасибо еще раз.
Тут у меня возникла еще одно затруднение, для выхода из которого также нужен толчок. Связано оно с первоначальным интегралом: нужно мне доказать еще одно неравенство. Для удобства выпишу все интегралы:
1)

2)

3)

Так вот, я хочу показать, что

.
Я так понимаю, что, наверное, проще всего доказать,

, что автоматически приводит меня к тому, что я хочу. И, как я понимаю, надо разложить

по формуле Эйлера по экспоненте. Но вот какую потом замену произвести, чтобы получить

и как вообще вылез
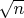
?
Или я что-то недопонял?