m$ писал(а):
akaWild писал(а):
И ещё один, если позволите, вопрос (надеюсь, заключительный

), как некое уточнение:
Здесь вероятности попарных пересечений означают то, что сразу у обоих человек будет по паре белых шаров? Или я ошибаюсь? Если да, то как преобразиться формула

, если в корзине всего 3 белых шара, а человек двое? Уберётся часть формулы после знака "минус"? Или всё-таки никак не изменится? Если вас сильно не затруднит, пожалуйста, разъясните этот момент.
Видимо, это вопрос мне, а не
$ 
.
Именно так, Вы не ошибаетесь. Если белых шаров всего три, то вместе события

и

при
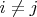
случиться не могут, и отнимать от суммы вероятностей будет нечего. В уменьшаемом изменятся биномиальные коэффициенты - будет

, а не из четырёх.
Да, я именно так и подумал, что ваш вопрос о том, с какой вероятностью у двух человек будет по паре тузов после раздачи.
На другие случаи это можно легко пересчитать, если вновь сосчитать число благоприятных исходов.
Добавлено спустя 4 минуты 38 секунд:akaWild писал(а):
Спасибо. Всё, вроде теперь во всём разобрался.
Хм, снова небольшое уточнение.Если в корзине 4 белых шара, а человек трое, то какой вид примет формула вероятности? Ведь, я так понимаю, здесь имеется три случая
попарных пересений: у первого человека 2 белых шара и у второго; у 1 и 3; у 2 и 3 (других вариатов нету, так как шара всего 4). Или формула остаётся неизменной, просто подсталяем вместо m число 3 и всё "разруливает"


?
Если вы будете применять то что я написал, число игроков - n у меня просто параметр. Разные n и вы получаете вероятности для этих разных случаев.
Обьяснения второго советчика - я в них не вникал. Чего то про "условные вероятности", формулы толи Байеса то ли еще кого применял повидимому.