фактор кольцо
![$Z_2[x]/x^2 $ $Z_2[x]/x^2 $](https://dxdy-02.korotkov.co.uk/f/1/d/0/1d0290c97d5178ed4339c2f9160998f582.png)
изоморфно самому себе?
С какой это радости?
Как это обосновать так, что бы препод поверил что я понимаю о чем говорю

Перевестись на гуманитарный факультет

Кстати, вот это кольцо:
![$\mathbb{Z}_2[x]/(x^2) \cong \mathbb{Z}_2[x]/(x^2+1)$ $\mathbb{Z}_2[x]/(x^2) \cong \mathbb{Z}_2[x]/(x^2+1)$](https://dxdy-01.korotkov.co.uk/f/8/1/b/81bd7c67442f6b9cd9ba3d5d0169dcf482.png)
... Первый раз такое вижу. Если положить

,

,

и

, то по сложению получается группа

(с образующими, к примеру,

и

), но умножение какое-то странное:

,

,

. Это кольцо имеет какое-нибудь специальное название?
P. S. В двух других случаях получаются кольцо

и поле
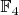
, с ними вроде как всё понятно...