Oo
чего-то я не понимаю в этой жизни. нет я конечно благодарен, но все равно не могу понять. допустим мы сделали такие преобразования z'=z, x'=(3x+4y+5)/5, я так понял приводим к
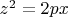
что есть р в данном случае, и куда девается y?
не поймите неправильно, халявы я здесь не ищу, просто хочу разобраться, этот единственное задание, которое у меня ну никак не могу решить или, что-то не так понимаю, или все проще чем я думаю =/