Многие из решений симметричны, поэтому совмещать можно по элементам симметрии. Например, случай

имеет у Слона симметрию

. Если спроецировать все точки на икосаэдр, то

точек сядут на его вершины, а ещё

- на середины его рёбер, разбивая каждую грань икосаэдра на четыре равных треугольника. В каждом из этих

треугольников располагается ещё по три точки:

Это решение аналогично решениям для

и

; по-видимому, располагая в каждом из

маленьких треугольников последовательно

точек, мы получим целое семейство подобных решений симметрии

(первые два случая

и

вырождены в

).
Случай

тоже имеет симметрию

:
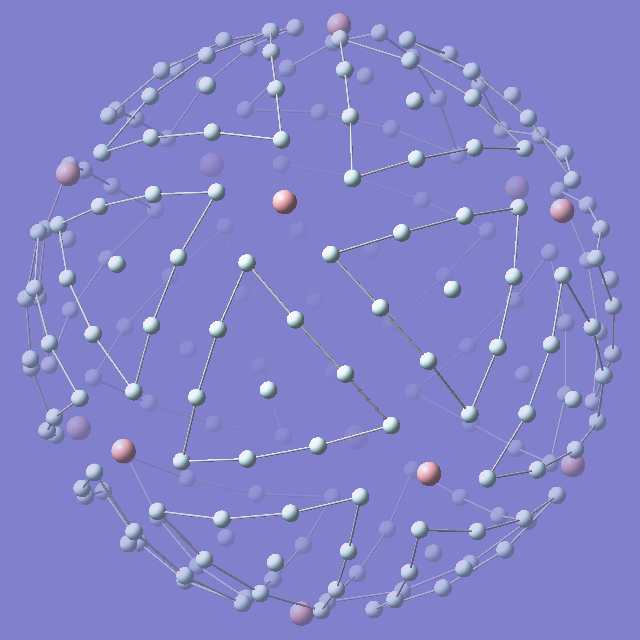
Он, судя по всему, является членом другого семейства решений, полученных размещением внутри каждой грани икосаэдра последовательно

точек (при этом

; симметрия вырождается в

для

и

).
Случай

(снова симметрии

) может быть получен из случая

; добавление новых и новых концентрических "пятиугольников", по-видимому, также даёт последовательность подобного рода решений (

):

Интересно, что случай

принадлежит также предыдущему семейству решений; он был упомянут в этой ветке
выше.
А случай

имеет ещё более высокую симметрию

:

точки проецируются в вершины,

- в центры граней и

- на рёбра (по две точки на каждое)
вот этого многогранника. Таким образом, каждой его грани принадлежат

точек; для

точек получаем соответственно решения симметрии

для

(обратите внимание, мы снова получили пересечение с ранее полученными семействами для

и

).
Похоже на то, что подобным образом можно построить дерево всех решений симметрии

или

. В основании будет

, затем разветвление на

и

и т.д.
Если построить такие деревья для всех точечных групп симметрии, то, возможно, удастся классифицировать всё множество решений задачи Томсона. Правда, к сожалению, большинство решений имеет низкую симметрию. Например, решения для

имеют симметрию

соответственно.
R.Deyanov, судя по тому, что расчёты Слон делал 16 лет назад, на современном компьютере его программа была бы вряд ли медленнее Вашей
