Здравствуйте,уважаемые пользователи форума. Решая следующие задачи у меня возникли некоторые вопросы , если вы сможете помочь мне разобраться-буду очень признателен
Задача №1
У преподавателя есть 36 экзаменационных билетов, пронумерованных 1,2,...,36.
Студент тащит 3 билета,какова вероятность того,что билеты вытянутые студентом окажутся из первой четверки
Событие

- студент тащит 3 билета из первой четверки

=

=

=

я вижу ,что это решено неверно, т.к для обратного события

=

=

Не пойму , где я допустил такой промах в рассуждении
Задача №2
Типография отправила газеты в 2 почтовых отделения . Вероятность своевременной доставки газет в каждое отделение равно 0.9 . Найти вероятность того , что 1) только одно отделение получит газеты вовремя
2)Хотя бы одно получит газеты вовремя
событие

- вероятность своевременной доставки газет в первое отделение

=

событие

- вероятность своевременной доставки газет во второе отделение

=

событие

- вероятность доставки газет только в одно отделение

=

=

пункт 2 (хотя бы одно вовремя) вызвал вопросы , я решил так
событие

обратное нашему условию - т.е все получат с опозданием

=

=

тогда вероятность нашего события равно

#3
Из коробки №1 содержащей 2 белых и 3 черных шара, переложили в коробку №2 3 шара , коробка №2 до этого содержала 4 белых и 4 черных шара . найти вероятность вынуть из второй коробки белый шар
событие

из второй коробки будет вынут белый шар.
гипотезы

переложили 2 белых и 1 черный

переложили 1 белый и 2 черных

переложили 3 черных

=

=


=

=


=

=


=
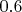

=


=
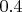

=

=

Задача №4
Два прибора производят детали ,которые поступают на конвейерную линию.
Производительность первого в трое больше чем второго. Вероятность изготовления качественной детали первым прибором равна 0.9 а вторым 0.7
с конвейера берется любые 5 деталей,найти вероятность того,что 4 из них годные
Тут я к сожалению не справился.... единственное что точно, что ее сказали решить через биномиальное распределение...Прошу вас помочь..
Задача №5
Вероятность покупки браковоной детали равна 1 %. каковы шансы на то,что среди 200 покупок окажется не более 4 бракованых деталей

=


=


=
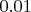

=

=


=

=

=

Подскажите мне пожалуйста все ошибки и недочеты,надеюсь что мне смогут помочь!=)