Хотите ли знать, как квантуется СТО?
Хотите знать, как электрон за его классическое время облетает всю Вселенную?
Для этого надо понять, а что же такое квантуемая скорость.
Цитата:
Имхо, путанице в обозначениях, понятных лишь ув. автору.
Это просто и понятно.
Начнем с рисунка:
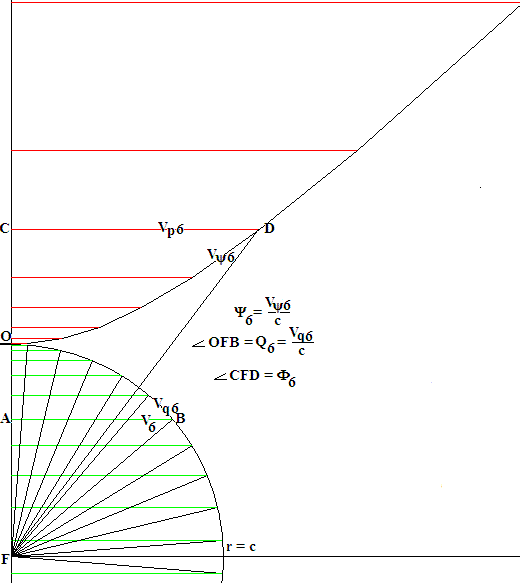
На рисунке показаны наборы 4-х видов скоростей при N=10. На самом деле большое квантовое число N значительно больше.
Скорости равной нулю нет. Скорости света для массивных частиц тоже нет. Набор скоростей соответствует ряду чисел: 0,5; 1,5; 2,5…, но мы обозначим скорости индексами 1, 2, 3,..
Проследим за скоростями, соответствующими квантовому числу 6.
Координатная скорость - отрезок АВ. Координатную скорость все, слава Богу, знают

.
Вторую скорость, которую давным-давно знают физики-релятивисты, называют быстротой. Вот связь между координатной скоростью, параметром быстроты

, и быстротой

:

. Быстрота аддитивна. При устремлении координатной скорости к скорости света, быстрота и её параметр стремятся к бесконечности. Быстроте на рисунке соответствует комплексная длина дуги OD. Параметр быстроты получаем делением этой дуги на скорость света, записанную в тех единицах, в которых вы работаете.
Третий вид скорости, называемый собственной скоростью (proper velocity), уже знают англоязычные физики-релятивисты, но русскоязычные писатели Википедии пока запаздывают. Обозначим её той же буквой v, снабдив индексом p от английского proper,

. Физический смысл: Отношение перемещения

к интервалу времени по собственным часам движущегося объекта

,

. К этому виду скорости я пришел лет двадцать лет назад. Проверено, - мин нет. Согласно статье в Wikipedia, физики ускорительщики тоже с удовольствием пользуются этой видом скорости. Пределом собственной скорости тоже является бесконечность. На рисунке собтвенная скорость

показана oотрезком CD. Формула связи с быстротой следует немедленно из геометрических соображений:

.
Четвертый вид скорости, квантуемая скорость, получен мной несколько лет назад. Квантуемой скорости с квантовым числом 6 соответствует длина дуги OB. Из геометрических соображений немедленно следует её связь с координатной скоростью:

Параметром квантуемой скорости является угол OFB,

.
Повороту осей систем координат соответствует угол CFD. Этот угол, как мы видим, не равен повороту

.
Продолжение следует, если модераторы и ускорительщики позволят это сделать.
------
Цитата:
Неужто некая точка троса (например, середина, но это неочевидно, а значит, и необязательно имелось в виду топикстартером) закреплена в шарнире?
Столб в системах обеих разлетающихся ракет находится за соответствующими горизонтами событий. То есть, столб действительно похож на шарнир. Но стоит какой то из ракет прекратить ускоряться, катастрофы столбу не избежать.
Цитата:
И трос абсолютно упругий (кстати, это как: нет остаточных деформаций? или абсолютно жёсткий?).
Очень послушный. Как только световой конус от ракеты касается того места, где должна быть соответствующая частичка троса, и говорит "брысь на место!", она мгновенно туда влетает. Но поскольку столб находится за пределами световых конусов, то он никуда не улетает, хотя и остается бесконечно долго быть прявязанным тросами к разлетаюимся ракетам. Пока ракеты за горизонтами, на рисунке мы видим три троса. Это конечно невозможно. Но эта же невозможность ограничивает и само непрерывное бесконечно долгое ускорение ракет.