Пусть имеется последовательность

независимых одинаково распределённых сл. величин таких что

для всех

. Пусть

- это плотность распределения

. Введем

и

- два марковских процесса, где

- константы, и

- тоже фиксированные числа, а

- некоторая известная функция, определенная на

и принимающая значения на интервале

;

- это возведение

в степень

. Очевидно,
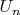
и

- зависимы. Рассмотрим 2-мерное блуждание

, и следущий момент выхода

, где

- заданные константы. Другими словами,

- это момент когда блуждание

впервые выходит за границы квадрата

начавшись в точке

. Интересует среднее
![$E[T_{A,B}^{v,u}]$ $E[T_{A,B}^{v,u}]$](https://dxdy-01.korotkov.co.uk/f/c/2/5/c2573ce2a050492deda54a7011ec20c182.png)
, а точнее правильность и результат следующих рассуждений относительно уравнения которому
![$E[T_{A,B}^{v,u}]$ $E[T_{A,B}^{v,u}]$](https://dxdy-01.korotkov.co.uk/f/c/2/5/c2573ce2a050492deda54a7011ec20c182.png)
должна удовлетворять.
1. Зафиксируем

. Рассмотрим

. Тогда

2. Пусть

. Эта величина очевидно не зависит от

. Тогда используя марковость

и
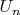
, можно записать

где интеграл берется по области

.
3. Далее, используя
![$E[T_{A,B}^{v,u}]=\sum_{k\ge0}P(T_{A,B}^{v,u}>k)$ $E[T_{A,B}^{v,u}]=\sum_{k\ge0}P(T_{A,B}^{v,u}>k)$](https://dxdy-04.korotkov.co.uk/f/3/a/1/3a10b8ba494385dd809e3136f0f168ae82.png)
, и то что

можно получить
![$$
E[T_{A,B}^{v,u}]=1+\int\int\frac{\partial^2}{\partial x\partial y}F(x,y|v,u) E[T_{A,B}^{x,y}]\,dx\,dy,
$$ $$
E[T_{A,B}^{v,u}]=1+\int\int\frac{\partial^2}{\partial x\partial y}F(x,y|v,u) E[T_{A,B}^{x,y}]\,dx\,dy,
$$](https://dxdy-01.korotkov.co.uk/f/c/8/6/c86844f02a25268834f96355f4f680d182.png)
где интеграл берется по области

.
Есть ли здесь ошибка? Спасибо.
|
i |
от модератора AD: |
| Сделал заголовочек темы поинформативнее. |