Геометрия ВТФ

[Nikop]

Лукомор в сообщении #331797 писал(а):

Nikop в сообщении #331778 писал(а):

Где ошибка?

Очевидно, в консерватории что-то подправить необходимо...

Ну это же не ответ :(

[Лукомор]

Nikop в сообщении #331760 писал(а):

Меня беспокоит привидение

Вот и ошибка...
На самом деле привидений не существует...
В заголовке ошибка - к ВТФ ваша геометрия отношения не имеет.

[Nikop]

Лукомор в сообщении #331801 писал(а):

Nikop в сообщении #331760 писал(а):

Меня беспокоит привидение

Вот и ошибка...
На самом деле привидений не существует...
В заголовке ошибка - к ВТФ ваша геометрия отношения не имеет.

Извините, за отнятое время.

[r-aax]

Nikop в сообщении #331793 писал(а):

r-aax в сообщении #331787 писал(а):

По-моему, натуральных $A$, $B$ и $S$ в том виде, в каком они изображены на рисунке, вообще не существует.

80^2 + 60^2 = 100^2 (10 ^ 4)

Да и спасибо за внимание, а то меня уже кретином окрестили )

На рисунке продолжение стороны $A$ попадает в угол прямоугольника. Таких натуральных $A$, $B$, $S$ не существует.

[ananova]

Nikop

Я не отвечу на Ваш вопрос, а только выскажу свою точку зрения по данной теме в форме рассуждения (вопросов и ответов к самому себе).

Если рассмотреть ВТФ в разных конечных полях (порождённых разными числами), то в степени 2 (в специально подобранном поле), можно считать, что мы имеем множество квадратичных вычетов, которые образуют элементы тройки: $x, y , z$. (О квадратичных вычетах можно почитать в Википедии).

При этом квадратичные вычеты образуют мультипликативную группу, т.е. результат сложения элементов поля не обязательно будет одним из элементов группы, т.е. будет квадратичным вычетом, а вот результат произведения обязательно будет таковым.

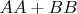
Т.е. $A+B$ может не быть квадратичным вычетом, а $AB$ - всегда будет квадратичным вычетом. Также, как и $AA$, и $BB$, будут квадратичными вычетами, а $AA+BB$ может не быть квадратичным вычетом.

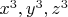
$x^3, y^3, z^3 $можно рассматривать (в специально подобранном поле), как 3-степенные вычеты (степени 3).

Для меня 3-степенные вычеты и 2-степенные вычеты - это инструмент, который помогает разобраться в Вашем примере.

Кроме того, результат сложения 3-степенных вычетов может быть решением сравнения Ферма (подчёриваю - решением сравнения, а не уравнения).

По-моему, если существует результат решения сравнения в 3-степенных вычетах, то при этом не обязательно должно существовать решение для квадратичных вычетов. Более того, сомнительно утверждать, что найденные, как решение, 3-х степенные вычеты будут совпадать с какими-то квадратичными вычетами (других чисел - не из данной тройки чисел), включая результат операции сложения.

Таким образом, делаю для себя заключение - искать решение уравнения Ферма в поле квадратичных вычетов,ошибочно, т.к. найденные решения в нём будут отличаться от решений сравнений 3-степенных вычетов. Возможно, это ставит новые вопросы, но ответ на них то мы знаем, благодаря доказательству Уйалса. Хотя, для решения проблемы на уровне сравнений, было бы интересно покопаться.

[AD]

Тема перемещена в карантин.
Nikop, оформите формулы в $\TeX$е. Введение здесь.
Для редактирования своих сообщений воспользуйтесь кнопкой .
Как исправите - пишите сюда, чтобы тему вернули.