Можно доказать. Можно даже выписать явное представление:
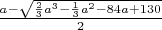
, где

.
Великолепно! Огромное спасибо. Быстро, информативно,
со вкусом. Особенно интересен, кубический полином под
радикалом. Это для меня просто открытие. Если нетрудно,
пожалуйста найдите еще выражение для такого бесконечного
радикала:
