Ну раз уж пошла такая пьянка -- поясню, почему я назвал утверждение в этой задачке "очевидным".
Пусть задан набор равноотстоящих узлов

,

(или, что эквивалентно, членов некоторой арифметической прогрессии). Конечные разности порядка

для функции

определяются рекуррентно:

;

.
С другой стороны, для них есть явная формула:

(между прочим, довольно очевидная: биномиальные коэффициенты, т.е. элементы треугольника Паскаля, подчиняются как раз примерно аналогичным рекуррентным соотношениям).
Так вот, есть такая теоремка: существует такая точка

, что

(при условии достаточной гладкости функции, естественно).
А сумма, предложенная в задаче -- это не что иное, как разделённая разность для функции

(с точностью до знака). Откуда моментально и ответ: эта сумма не равна нулю при всех
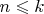
(кроме исключительных случаев) и равна нулю при всех

.
Несколько из пушки по воробьям, конечно. Зато очевидно.
-- Пн мар 15, 2010 09:52:22 --Дифференцируем ее k раз и получаем, что ее производная порядка

записывается так:

Следовательно наше выражение (мое тождество) - это производная k-го порядка от функции

в точке 0.
Весьма разумно (с точностью до выбора буковки

в качестве индекса).