Имеется

мишеней. За каждую стрельбу стрелок попадает в

случайно выбранных мишеней. Всего проводится

стрельб. Требуется найти
а) Наиболее вероятное количество мишеней в которые хотя бы один раз попадёт стрелок (за

стрельб).
б) Вероятность того, что количество мишеней в которые хотя бы один раз попадёт стрелок равно

.
Проще представить последовательность стрельб как матрицу размера

на

, в каждом столбце которой маркируется произвольно

элементов. Требуется найти
а) Наиболее вероятное количество строк в которых есть хотя бы один маркированный элемент.
б) Вероятность того, что количество строк в которых есть хотя бы один маркированный элемент равно

.
Как решить задачу, если значение

- с каждой стрельбой резное, то есть

представляет собой случайную величину с заданным распределением?
Я пробовал решить эту задачу (вопрос б с фиксированным

) следующим образом. Пусть

- количество выбранных на

-ой стрельбе мишеней, в которые ещё не попадал стрелок на предыдущих стрельбах (возможно, что

для какого-либо

). Очевидно
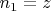
, а так же, что сумма всех

есть

. Тогда не сложно посчитать количество вариантов стрельб, отвечающих заданному набору

. Останется посчитать количество вариантов таких наборов. Последняя задача фактически представляет собой задачу поиска количества вариантов разбиения натурального числа на заданное количество неотрицательных натуральных слагаемых, не превышающих определённое значение. Её я решить не смог и ответа не нашёл пока.