То есть можно рассматривать функции от "сколь угодно мощного множества переменных".
Ну да. Почему нет? Конституция, вроде бы, это не запрещает.
Но как это формально записать?
Например, так:

. Кстати, рациональные функции --- это не функции (т.е. не отображения), а просто некие формальные выражения. Формально можно так сказать. Поле рациональных функций от переменных

над неким полем --- это поле отношений (целостного) кольца многочленов от тех же переменных над тем же полем, а многочлены можно рассматривать как алгебру с базисом

, где в произведении

и

для всех
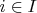
, кроме конечного числа (операции определяются естественным образом).
(да и нужная мощность будет гораздо больше

)
Если нужна мощность ровно

, то можно взять конечное поле (если

бесконечно). Вообще, если

--- поле,

--- множество,

(
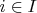
) --- независимые переменные, то

, если я не нагнал.
-- Пн 16.11.2009 05:21:39 --Для счётного - в виде формальных степенных рядов (?).
Это не так даже для двух переменных (как Вы разложите в ряд

?).
-- Пн 16.11.2009 05:30:38 --Если неформально, то можно так сказать. Вот у нас есть какое-то поле

. Мы усилием воли берём и добавляем к нему новые элементы

, а также всё, что получается из

с помощью применения конечного числа операций суммы, разности, умножения и деления.