Теперь сформулируйте, что такое совпадение двух плоскостей.
(Ведь осталось доказать, что направляющие подпространства для двух совпадающих плоскостей совпадают, а разность векторов сдвига лежит в направляющей плоскости.)
Плоскости Н и

совпадают, если им принадлежат одни и те же векторы (элементы пространства)...
Аха.
Т.е. если

, тогда сумма какого-то элемента направляющего попространства L с

должна равнятся сумме какого-то элемента направляющего подпространства

c

так...
если я обозначу базис базисные векторы подпространства

как

, которых n штук, а базис подпространства

как

, тогда, елси

то это означает, что для каждого

, найдуться такие

для которых

.
(где

и

- числа действительные или комплексные)... =) во загнул ))
ну если обозначить

, а

, тогда

...
А если еще и предположить что
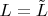
, то очевидно, что
(1)

,
что будет означать что

. А это означает (2)что у одной плоскости разница между ее вектороми сдвига всегда принадлежит направляющему подпространству.
А если наоборот предположить что

, то тогда из (1) следует что

что означает
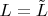
. А это означает (2) что у одной и той же плоскости обязательно совпадают направляющие подпространства...
т.е елси

, то тогда

, а из этого следует что

, что было показано выше )))
А если

и

, тогда из (2) следует что

.
Ура... надеюсь что ура )
похоже на правду хоть чуть чуть?