Кажется, таких

нет.
Обозначим

и введем

. Так как

- однородный, то

, где

. Тогда

. Искомый

существует, если и только если существует

и есть точка
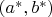

.
Сгруппируем члены с симметричными коэффициентами:

Тогда

- симметричный многочлен от 2-х переменных. Если есть точка, где этот многочлен меньше нуля, то он в точке минимума также меньше нуля. Попытавшись найти его экстремум обычным способом, приходим к выводу, что

, либо

, либо

.
Предположим последнее. Тогда

Но

, а

Поэтому случай

невозможен. Отсюда следует, что

имеет не более 2-х переменных.