количество сложений и умножений при вычислении формул

[st256]

Предположим, есть двуместные операции из $a$ и $b$ в $c$ - вычитание и сложение:
$c=a+b$
$c=ab$
доказано ли утверждение, что минимально возможное количество этих операций при вычислении формулы вида

$y=\sum\limits_{i=1}^{N} a_i x_i $

равно $2N-1$? И если доказано, то где?

[bot]

Очевидная идукция:
При $N=1$ выражение считается в одно действие.
Если $N>1$, то последнее действие - это сложение:

$\sum\limits_{i=1}^{N} a_i x_i =\sum\limits_{i=1}^{n} a_i x_i +\sum\limits_{i=n+1}^{N} a_i x_i $

Отсюда минимально возможное число действий - это $(2n-1)+(2(N-n)-1)+1)=2N-1$.

[Xaositect]

bot в сообщении #242368 писал(а):

Если $N>1$, то последнее действие - это сложение:

Почему?

[Профессор Снэйп]

Ага. Если все $a_i$-ые равны $0$, то ваще никаких операций не надо

Вообще, конечно, задача нуждается в основательной формализации. Что значит "операции при вычислении формулы"?

[bot]

Ну формализация понятна. Каково минимальное число действий, гарантирующее вычисление такой суммы при любых коэффициентах. Под действием понимаем либо сложение двух чисел либо их умножение.

-- Пт сен 11, 2009 17:49:03 --

Иначе говоря, пишем программу для компьютера, обеспечивающую вычисление всевозможных таких сумм. Компутер за один шаг выполняет только одно действие - либо складывает два числа, либо перемножает два числа. Каково наименьшее возможное число шагов работы компьютера по такой программе?

Профессор Снэйп в сообщении #242399 писал(а):

Ага. Если все -ые равны , то ваще никаких операций не надо

Надо и ровно столько же.

[Xaositect]

Ну да.
Известные методы получения "очевидных" нижних оценок в таких случаях очень интересны.
Если доказать, что сложений нужно не меньше $n-1$, просто: достаточно рассмотреть множество переменных $x_i$, от которых зависит функция, то с умножениями все хуже.

[bot]

Ну можно и совсем формально:
Сколько надо поставить пар скобок, чтобы выражение стало термом. Определение терма по индукции дать?

Xaositect в [url=http://dxdy.ru/post242396.html#p242396]сообщении #242396
[/url] писал(а):

Почему?

Ответил на вопрос?

[Xaositect]

bot в сообщении #242408 писал(а):

Ответил на вопрос?

А почему это выражение нельзя упростить?

[bot]

А как Вы это себе представляете? Впрочем, такого действие условием и не предусматривалось.

[Xaositect]

bot в сообщении #242425 писал(а):

А как Вы это себе представляете? Впрочем, такого действие условием и не предусматривалось.

Условем предусматривается минимальное кол-во операций для вычисления выражения и никак не указан их порядок или взаимное расположение.
То есть, если Вы говорите, что упростить выражение нельзя, нужно доказать, что его упростить нельзя(это можно доказать, я сейчас перечитваю Algebraic Complexity Theory и думаю, как бы это попроще изложить).

[rishelie]

видимо имеется ввиду максимум минимумов числа операций для всех таких выражений
только сдается мне, что если подставляемые числа заданы в явном виде или с помощью неких уравнений, то сия сумма будет считаться быстрее.

[st256]

Господа, должен вас огорчить. Эта задачка не столь тривиальна. Есть серьезные подозрения, что ее можно решать только перебором. Вариант с индукцией, к сожалению, неправильный. Вообще, последний из великих, кто рассматривал нечто подобное - Колмогоров. Сейчас с этим никто не работает. Толи не могут, толи просто не в курсе, что такие задачи есть...

Задачка попроще: за сколько операций сложения можно вычислить сумму вида:

$y=x+x+x+x+x+x+x+x+x+x+x+x+x+x+x=15x$

[Xaositect]

Вот нижняя оценка количества умножений:
Рассмотрим алгоритм, использующий сложения, вычитания и умножения, и вычисляющий $\sum\limits_{i = 1}^n a_i F_i(\vec{x})+F_0(\vec{x})$.
Будем считать "правильные" умножения, в которых хотя бы один из сомножителей зависит от каких-то $a_i$, и докажем, что их не менее $n$. По индукции.
База. $n=1$. Для вычисления $a_1 F(\vec{x}) + F_0(\vec{x})$ нужно одно правильное умножение.

Переход. $n>1$. Пусть алгоритм имеет сложность(кол-во правильных умножений) $c$. Рассмотрим первое правильное умножение. Оно вычисляет произведение $(\sum\limits_{i=1}^n \alpha_i a_i + A(\vec{x}))(\sum\limits_{i=1}^n \beta_i a_i + B(\vec{x}))$. Без ограничения общности $\alpha_1 = 1$.
Рассмотрим новый алгоритм, который работает так: сначала он вычисляет $a_1 = - \sum\limits_{i=2}^n - A(\vec{x})$, а затем работает так же, как исходный. Так как в этом случае $(\sum\limits_{i=1}^n \alpha_i a_i + A(\vec{x})) = 0$, первое правильное умножение можно убрать, т.е. мы получили алгоритм вычисления какой-то функции $\sum\limits_{i=2}^{n}a_i G_i(\vec{x}) + G_0(\vec{x})$, имеющий сложность $c-1$. По предположению индукции $c-1\geq n-1$.

-- Пт сен 11, 2009 19:22:17 --

Тут есть неточности, но их в принципе можно устранить (например, надо указать, что $F_i$ должны быть неконстантными, линейно независимыми и проверить это для $G_i$)
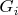
Это изложение на основе статьи Винограда "On the Number of Multiplications Required to Compute Certain Functions" и шестой главы "Algebraic Complexity Theory", авторы Burgisser, Clausen, Shokrollahi.

-- Пт сен 11, 2009 19:27:10 --

st256 в сообщении #242453 писал(а):

Задачка попроще: за сколько операций сложения можно вычислить сумму вида:

Конкретно для 15 я уже не помню значение. Для $n$ есть оценка $\log n + \frac{\log n}{\log \log n} (1+o(1))$

[maxal]

st256 в сообщении #242453 писал(а):

Задачка попроще: за сколько операций сложения можно вычислить сумму вида:

$y=x+x+x+x+x+x+x+x+x+x+x+x+x+x+x=15x$

Ответ на подобные задачи дают аддитивные цепочки.
http://en.wikipedia.org/wiki/Addition_chain

[st256]

Ночь, наверное поэтому торможу. Что такое "правильные" умножения? Как понять, что сомножитель сам от себя зависит?

Xaositect в сообщении #242455 писал(а):

Будем считать "правильные" умножения, в которых хотя бы один из сомножителей зависит от каких-то $a_i$, и докажем, что их не менее $n$.

-- Пт сен 11, 2009 21:43:11 --

Вообще-то Вы привели алгоритм Винограда, а он только умножения вроде бы учитывает....

-- Пт сен 11, 2009 21:45:04 --

maxal в сообщении #242460 писал(а):

st256 в сообщении #242453 писал(а):

Задачка попроще: за сколько операций сложения можно вычислить сумму вида:

$y=x+x+x+x+x+x+x+x+x+x+x+x+x+x+x=15x$

Ответ на подобные задачи дают аддитивные цепочки.
http://en.wikipedia.org/wiki/Addition_chain

Нифига они ответа не дают. Эта классический случай, когда задача решается перебором. Я ее привел, чтобы показать, почему не работает метод мат. индукции на более сложном примере.