Анализ ур-ний ВТФ для простых степеней N покажем на примере N=3, для лучшего понимания способа доказательств.
Дано:

,

-делится на 9, т.есть









или

Примем

.В ур-нии (5)

заменим на

,получим:

,проведем сокращения и преобразуя,получим:

. Примем

,заменим

и сократим на 27,имеем:

,т.как все члены данного ур-ния делятся на

,значит и

,т.есть

.
Поэтому

и т.как

делится на 9,то и

делится на 9.
Уравнение (6) приведем к виду:

(9).
Уравнение (7) приведем к виду :

.-делится на

,(10) (здесь отбросили все члены,которые делятся на

и более).Так же поступим и с ур-нием (8),имеем:

, -делится на

.

, (11)

, (12)

подобно (12).Запишем(10),учитывая(11) и (12),отбросив все члены,которые делятся на

, как выражение:

,-делится на

(13).
Из (13) вычтем (9),имеем:

, (14) и

, (15).
Из выражения (15) вычитаем (14),получим:

,отбросим все члены,которые делятся на 27,проведем преобразования,имеем:

,-делится на 9, или

, и

,-должно делится на 9, но

делится на 9, т.как из(6),если

делится на 9,то

делится на 9 и более и

делится на 9. Если принять

делится на 9,то

должна делится на 9,так как

делится на 9.Поэтому и

будет делится на 9 и снова

делится на 9. Поэтому и 12t должен делится на 9,что противоречит условию:
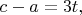
при

.
Если принять

,то

.проведя новый анализ при данных условиях,получим:

должна делится на 27 и так до бесконечности.
И так,доказано,что если х или у делится на 9 и более,решения уравнения Ф. для N=3 в целых числах нет. Таким же методом доказывается и случай,когда z делится на 9 и более.
Если данные выкладки верны,то можем утверждать:ВТФ решена на елементарном уровне,т.как доказательство для всех простых степеней N аналогично приведенноиу.
Формулы для анализа (z-делится на 9) имеют другой вид.[

] Приводить доказательство для z делится на 9 ,уже не интересно,главное-в чем я заблуждаюсь в данной статье.