Стрелочками это же Вы не биекцию и произвольное отображение, а "тогда и только тогда когда" и "следует" обозначили? И

и

в первой половине имелись в виду с большой буквы?
Да, в таком контексте

это импликация, а

- эквивалентность.
И да, слева и справа

и

в одинаковом регистре должны быть.
Да это по-моему просто определение равных множеств
Это аксиома про связь значков

и

. Она состоит из двух частей:
1. Если множества равны, то им принадлежат одни и те же элементы.
Это частный случай так называемых "логических аксиом равенства". По умолчанию считается, что если в языке используется знак

, то там есть и аксиомы вида
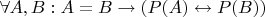
для всех возможных формул

. Они относятся к "логическим" аксиомам (в противоположность "предметным"), потому что в общем-то ничего содержательного о нашей теории не говорят.
2. Если множествам принадлежат одни и те же элементы, то множества равны.
Это как раз содержательная часть. В принципе можно было бы сказать, что у множеств есть еще какие-то характеристики, и есть много разных множеств с одними и теми же элементами.
Следствие "мн-ва равны" ложно, если, насколько я помню, ложна причина
Нет, это импликация в другую сторону. В данном случае она тоже есть (потому что в аксиоме эквивалентность), но в общем случае ее может и не быть.
икс - какой-либо в самом широком смысле? Я такого ещё не видел, если честно
Как раз в самой базовой формализации все кванторы неограничены (т.е. квантор не накладывает ограничений на переменную). Как раз запись вида
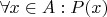
определяется через неограниченные кванторы:
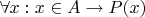
.
(Оффтоп)
Эту теорию Лектор в начале упоминал. Там ещё ZFC по-моему есть
Да, есть. Это, наверное, самая популярная из формальных теорий множеств. И почти вся математика работает с чем-то, что можно условно назвать "неформальной ZFC".
Разница между ZF и ZFC будет позже. В анализе почти всегда используется имено ZFC, причем явно использование C обычно даже не проговаривается.
Есть теорема, что при удалении одного элемента из бесконечного множества его мощность не меняется
Это, например, теорема ZFC, но не ZF.
Ограничиваясь этой задачей, можем считать что "ничего" это тоже подгруппка кубиков, а можем не считать. Вот если не считать, то ведь мои соображения верны?
Это другая задача - существует ли биекция между

и
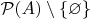
.
Она опять же не существует если

. Предположите, что диагональный метод выдал пустое множество, и для каких-нибудь

и

посмотрите на прообразы
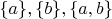
.