Ну или семейство спиралей. Мои познания в математике поверхностные (инженер-механик), да и на пенсии, учиться и поздно и ни к чему уже, обращаюсь зв помощью.
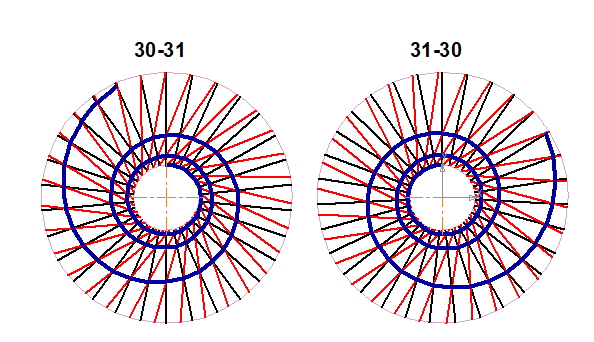
Над картинками вверху первая цифра количество чёрных отрезков, через черточку красных. "Наткнулся" я на них именно в геометрическом виде строя массивы отрезков относительно точки (это команда так называется в чертёжной программе). Саму спираль проводил по точкам кривой Безье (она плавность придаёт).
То есть совершенно случайно обнаружил, немного позднее вывел и формулу для них (на удивление простой оказалась).

=
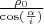
или вот так складней будет
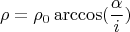

- текущее значение радиус-вектора (так кажется?) спирали,

- радиус начальной окружности,

- угол пройденный радиус-вектором,

в случае геометрического представления спирали (точки на пересечениях отрезков прямых) целое число, при построении по точкам - любое.
Странное дело - ни поиск по запросу "математические спирали", ни по картинке не дали полного совпадения. Неизвестна такая спираль что ли? Правда она начинается не из начала координат, а из точки на начальной окружности, но всё равно странно. Ну, формат поста велит закругляться, добавлю только ссылки, где можно ознакомиться подробнее.
https://dzen.ru/a/aBZbQ9ualkPlGcrAhttps://dzen.ru/a/aDGuz6KhK14AKAtMhttps://dzen.ru/a/aOUFBSDO-AAgCtqL