Пробую решать "олимпиадные" задачи, пока только для седьмого класса (ну ладно, девятого). Хотел узнать верны ли рассуждения.
Цитата:
Найти наибольшее и наименьшее натуральное

такое что
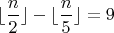
(Оффтоп)
Я обратился к теореме о делимости целых, в соответствии с которой
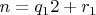
при этом
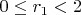
и
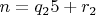
, при этом
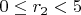
.
Тогда
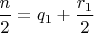
, а
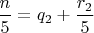
и получается что по условию
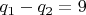
.

и

зависят от

и тогда нужно найти наибольшее и наименьшее

при которых равенство верно.
Выразим

через

и подставим в равенство:
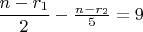
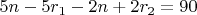
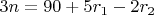
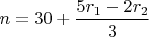
, при этом
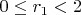
и
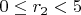
И вот тут я не понял, нужно перебирать пары остатков

и

от наибольшего для нахождения наибольшего (т.е. рассматривать при
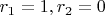
, потом
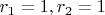
- и так пока не получится первое целое

) и аналогично для наименьшего (т.е.
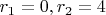
, потом
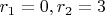
- и так пока не будет целое)? Ну а если бы делители, и как следствие остатки могли бы варьироваться в большем диапазоне? Можно было тогда просто сразу

подбирать без всех этих теорий делимости.
Есть предположение что достаточно взять пару остатков дающую наибольшее и наименьшее, даже если

получается нецелым, и тогда целая часть будет всегда совпадать с

для пары остатков дающих наименьшее\наибольшее целое

, ну и тогда перебирать ничего не нужно.
Ещё конечно есть идея "продиференцировать" выражение с остатками как функцию двух натуральных (целых) переменных и найти на нужном интервале нули (в нулях же, насколько я понимаю, производная, а точнее функция скорости в данном случае, показывает в какой точке у первообразной экстремум)