Решал олимпиадную задачу для шестого класса, в итоге по сути так и не решил, хотел бы получить советы как нужно было действовать в целом и на конкретных этапах.
Цитата:
Найти все десятичные числа

и

, состоящие из двух цифр, произведения
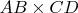
которых есть десятичное число из трёх цифр
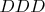
Не буду приводить решение в той последовательности в которой оно было, поскольку делал много ошибок, и вообще решал задачу неделю.
Я решал сначала, рассматривая за основу умножение в столбик двухцифровых чисел но не "по модулю 10", потому что вычетов на лекциях ещё не было и я почти ничего об этом не знаю, а типо в "поле характеристики 0", ну то есть в обычных числах.
Сначала проанализировал такое умножение, получив следующие свойства:
(Оффтоп)
1. Чтобы единичный разряд результата умножения был

, необходимо, чтобы единичный разряд
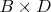
был

. Для нечётных

, кроме

с учётом того что все числа

натуральные (пока целые) и меньше десяти, это возможно только если

. Для чётных

,

может принимать два значения:

и

. Для

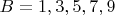
.
2.

, поскольку нужно получить число из трёх цифр.

, иначе единичный разряд произведения

. Ни

ни

не ноль, поскольку тогда это не двухцифровые числа. Тогда
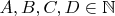
и меньше десяти.
3. Поскольку по условию результат умножения - число именно из трёх цифр, то
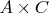
, отвечающее за сотенный и тысячный разряды обязано быть меньше десяти.
4. Поскольку сотенный разряд умножения должен быть

, то
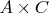
должно быть меньше либо равно

.
5. Если
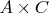
равно

, то нужный сотенный разряд уже достигнут только за счёт них, и тогда
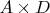
и
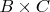
, обеспечивающие десятковый разряд, не должны переполнятся. Но каким-бы не был

,
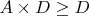
, и тогда
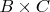
(на самом деле ещё потенциально

переполнение от

) должно "переполнить"
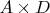
(поскольку

не может быть нулевым), чтобы "дойти" до

. Значит переполнение десятков всегда будет происходить, и переполнятся десятки будут на разряд сотен. А по предположению
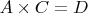
, к сотням больше ничего добавляться не должно. Противоречие.
Значит
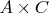
строго меньше

.
6. С учётом того что
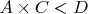
,

и

и по отдельности меньше

.
Теперь переходим от теории чисел к алгебре. Я решил записать три уравнения для каждого из разрядов нужного произведения. Поскольку арифметика по вычетам мне не известна, нужно решать всё в обычных числа, которые по отдельности могут "переполнять" десятку, но уравнения в изначальном виде гарантировано должны давать выражения меньшие

, а точнее ровно

. Получилось (с седьмой где-то попытки) так (далее я не буду писать знак умножения, т.е.

означает

, и может быть больше десяти. Также, далее везде под квадратными скобками
![$[]$ $[]$](https://dxdy-01.korotkov.co.uk/f/c/a/b/caba7d3b8508a5a054a5119af5020fa982.png)
будет иметься в виду не ближайшее целое, а нижняя целая часть

):
(Оффтоп)
Единицы:
![$BD-10[\dfrac{BD}{10}]=D$ $BD-10[\dfrac{BD}{10}]=D$](https://dxdy-01.korotkov.co.uk/f/4/e/b/4ebbeaf25d4d538487741e7e166b4b5982.png)
Десятки:
![$(AD+[\dfrac{BD}{10}]-10[\dfrac{AD+[\dfrac{BD}{10}]}{10}]) + $ $(AD+[\dfrac{BD}{10}]-10[\dfrac{AD+[\dfrac{BD}{10}]}{10}]) + $](https://dxdy-04.korotkov.co.uk/f/3/3/a/33aa0421c6d5ea1ba78a4f371f6a75ce82.png)
![$(BC-10[\dfrac{BC}{10}])-10[\dfrac{AD+[\dfrac{BD}{10}]-10[\dfrac{AD+[\dfrac{BD}{10}]}{10}] + BC - 10[\dfrac{BC}{10}]}{10}]=D$ $(BC-10[\dfrac{BC}{10}])-10[\dfrac{AD+[\dfrac{BD}{10}]-10[\dfrac{AD+[\dfrac{BD}{10}]}{10}] + BC - 10[\dfrac{BC}{10}]}{10}]=D$](https://dxdy-01.korotkov.co.uk/f/4/9/2/4924e0f9ea077d300afd545097569d4582.png)
Сотни:
![$AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]-10[\dfrac{AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]}{10}]=D$ $AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]-10[\dfrac{AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]}{10}]=D$](https://dxdy-01.korotkov.co.uk/f/4/9/2/4927c15b33b975e1d7e3b3dd1c90b99382.png)
Далее мне потребовалось следующее утверждение: если в выражении нижней целой части отсутствует вычитание нецелых, то как вычитающиеся так и прибавляющиеся целые можно вынести за знак нижней целой части. Доказательство: Пусть под знаком нижней целой части, нецелое с положительным знаком и целое:
![$[r\in\mathbb R + z\in\mathbb Z]$ $[r\in\mathbb R + z\in\mathbb Z]$](https://dxdy-02.korotkov.co.uk/f/1/f/7/1f7e0da44b2f1616f2e7674f382efef282.png)
. Тогда нецелое можно представить как сумму целого и нецелого больше либо равного нуля и меньшего единицы:
![$[(n\in\mathbb N + 0.x) + z]=[(n+z)+0.x]=n+z=[r]+z$ $[(n\in\mathbb N + 0.x) + z]=[(n+z)+0.x]=n+z=[r]+z$](https://dxdy-04.korotkov.co.uk/f/f/b/1/fb195c9d726525bacdb3b1823fd0659d82.png)
Используя это утверждение, сокращаем:
Единицы:
![$BD-10[\dfrac{BD}{10}]=D$ $BD-10[\dfrac{BD}{10}]=D$](https://dxdy-01.korotkov.co.uk/f/4/e/b/4ebbeaf25d4d538487741e7e166b4b5982.png)
Десятки:
![$AD+[\dfrac{BD}{10}] + $ $AD+[\dfrac{BD}{10}] + $](https://dxdy-04.korotkov.co.uk/f/b/9/c/b9c7ccb0153f7f0d6cc22a423a267a8582.png)
![$BC-10[\dfrac{AD+[\dfrac{BD}{10}]+ BC}{10}]=D$ $BC-10[\dfrac{AD+[\dfrac{BD}{10}]+ BC}{10}]=D$](https://dxdy-03.korotkov.co.uk/f/a/2/a/a2a3d8528d51e289c6425498c410c52c82.png)
Сотни:
![$AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]-10[\dfrac{AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]}{10}]=D$ $AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]-10[\dfrac{AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]}{10}]=D$](https://dxdy-01.korotkov.co.uk/f/4/9/2/4927c15b33b975e1d7e3b3dd1c90b99382.png)
По условию, сотни не должны переполнять, а значит
![$[\dfrac{AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]}{10}]=0$ $[\dfrac{AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]}{10}]=0$](https://dxdy-03.korotkov.co.uk/f/6/8/6/686ac085c706ba595ba4f2a0e5e2037182.png)
, и тогда сотни окончательно:
![$AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]=D$ $AC+[\dfrac{BC}{10}]+[\dfrac{AD+[\dfrac{BD}{10}]}{10}]=D$](https://dxdy-02.korotkov.co.uk/f/d/b/8/db887d812b636f7c418e9589fd4d63f182.png)
Выразим

через десятки:
![$A=1+\dfrac{10[\dfrac{AD+[\dfrac{BD}{10}]+ BC}{10}]-[\dfrac{BD}{10}]-BC}{D}$ $A=1+\dfrac{10[\dfrac{AD+[\dfrac{BD}{10}]+ BC}{10}]-[\dfrac{BD}{10}]-BC}{D}$](https://dxdy-03.korotkov.co.uk/f/2/3/e/23e2b639e2d430b6b3750435a89d6df282.png)
. Из чего делаем важное заключение, что:
7.

(а ещё выражение числителя должно быть делимо

).
Тут уже можно составить оценочную таблицу допустимых

:
(Оффтоп)
Получается, необходимо перебрать

комбинации, не учитывая

. Это намного меньше

, но перебирать столько всё равно не хочется, поэтому я пробовал дать более сильную оценку.
Были разные идеи, но то ли я запутался столько дней решая, то ли они были не достаточно обобщающими, и я решил уже перебирать, но только перед этим написать программу, которая выдаст все нужные числа и покажет все ли они удовлетворяют моим оценкам. Ну это не читерство, поскольку я просто хотел сверить будущий ответ. Я решил написать сценарий на Javascript, чтобы не компилировать, подвергаясь соблазну просто использовать просто eval(a+""+b+"*"+c+""+d), проганяя независимо все переменные, но решил всё же подумать. Ну и придумав код, понял что видимо придумал как это должен был решать шестиклассник, поэтому останавился на коде и вернулся к решению, теперь уже параллельно другим путём:
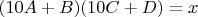
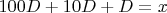
Тогда
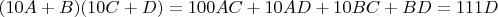
и к сожалению, я сделал ошибочный вывод, что
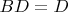
из которого последовало ошибочное

. После этого получается
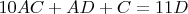
, но это всё равно по существу, решения - то есть уменьшения количества перебираемых комбинаций, не дало. Я много как крутил это выражение, например
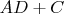
должно оканчиваться на

, тут я вернулся к целой части, записал как
![$AD+C-10[\dfrac{AD+C}{10}]=D$ $AD+C-10[\dfrac{AD+C}{10}]=D$](https://dxdy-03.korotkov.co.uk/f/6/e/5/6e5601f5b5f74972d3e286dde5e368c282.png)
и я также смог найти явное выражение
![$[\dfrac{AD+C}{10}]=[\dfrac{11D-10AC}{10}]=[1.1D-AC]=D-AC$ $[\dfrac{AD+C}{10}]=[\dfrac{11D-10AC}{10}]=[1.1D-AC]=D-AC$](https://dxdy-02.korotkov.co.uk/f/5/3/1/531f5f64c74f11259235e7ebf54ae6a682.png)
и тогда
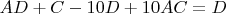
, но это уже хождения кругами. Пробовал ещё:
(Оффтоп)
Выразить

, ну в частности:
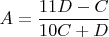
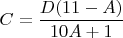
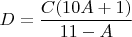
И как-то ограничить по признаку делимости, но толком ничего не получил. Ну и в итоге я всё-таки дописал программу и увидел.
Ещё, если

, то по ранееприведённому выражению
![$A=1+\dfrac{10[\dfrac{AD+ C}{10}]-C}{D}$ $A=1+\dfrac{10[\dfrac{AD+ C}{10}]-C}{D}$](https://dxdy-01.korotkov.co.uk/f/0/f/0/0f05c4065c962884ac99a0574ad68fe782.png)
, и если целая часть

, то получается что как бы обратный по сложению к

, но только "по модулю

" должен быть делим (не по модулю 10, а просто)

. Ну ещё числитель меньше
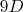
, но опять-таки развивая это ни к чему не привело.
Ещё заметил что вычеты можно рассматривать как циклы (перестановки), тема которых была на алгбере перед определителем.
Ну и в итоге я всё же дописал программу, которая, увы, помимо

, которые я ещё вначале подобрал, выдала вторую (и всё) пару

(а я же полагал что

только единица, хотя изначально рассматривал и, как раз

для

).