Anton_PeplovФункция, ряд Тейлора которой имеет бесконечное количество не равных нулю коэффициентов.
(Может быть я неправильно формулирую.)
У

и
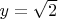
коэффициент один - при нулевой степени

.
У

коэффициент один - при второй степени

.

имеет бесконечное количество не равных нулю коэффициентов.
Зная свойства квадратного корня можно утверждать, что
1. При рациональном значении

значение

может быть как иррациональным, например
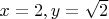
, так и рациональным, например
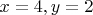
, т.е. существуют рациональные значения функции при рациональных значениях аргумента.
2. Рациональные значения

в виде дроби, числитель и знаменатель которой есть квадраты соответствующих натуральных чисел, и рациональные значения

в виде дроби, числитель и знаменатель которой есть эти натуральные числа, являются искомыми.
Вопрос в том, что можно ли прийти к выводам 1 и 2 непосредственно из коэффициентов ряда Тейлора (не преобразовывая ряд обратно в функцию) ?