У арифметики Пеано есть нестандартные (опять же) модели. Допустим, определим для объектов этой теории понятие мощности. Да и всех других недостающих понятий. Будет ли этого достаточно?
Возьмите стандартный текст по матлогике и проверьте. Я даже не понимаю, как вы в арифметике будете записывать фразы вида "групповая операция на множестве

— это отображение
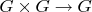
с такими-то свойствами." По-хорошему внутри арифметики вам нужно определить произведение "множеств", функции между ними, и выполнение всяких аксиом. Это уже кодирование какой-то декартовой категории внутри арифметики как минимум, а для интерпретации кванторов понадобится топос.
Просто подумалось, что вопрос невыводимости некоторого утверждения теории может быть сведен к определению его истинности в различных моделях.
Вопрос о невыводимости утверждения теории — это вопрос о несуществовании некоторого комбинаторного объекта (формального вывода). То есть речь идёт про истинность другого утверждения, в другой теории.
А сколько значков

вы для этого рисуете?
От модели нужно, чтобы каждую замкнутую формулу можно было в ней проверить на истинность (не обязательно конструктивно, просто хоть в каком-то разумном смысле). Замкнутая арифметическая формула — это просто строка из чисел, переменных, арифметических и логических символов, в ней не может быть никаких

.
-- 25.01.2026, 20:12 --Я пытаюсь сказать лишь то, что понятие истинности в модели столь же мутное, сколь мутно само понятие модели, ибо как раз восходит к первочерепахе по черепахам аксиоматических метатеорий (множеств или еще каких)
Это лишь говорит о неудобстве вашего взгляда на математику как бесконечной иерархии метатеорий.