Модель есть пара - множество и интерпретирующее отображение (см. Кейслер, Чэн, "Теория моделей", стр. 33). Стало быть, моделью может быть только объект исключительно некоторой теории множеств?
А почему Вы спрашиваете только про теорию моделей?
Группа - это множество плюс бинарная операция, подчиненная трем общеизвестным аксиомам. Нужна ли теория множеств для изучения теории групп?
Линейное пространство - это множество

плюс поле

(которое тоже множество + две бинарные операции) плюс функция
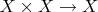
и функция
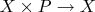
, подчиненные общеизвестным аксиомам. Нужна ли теория множеств для изучения линейной алебры?
Вероятность - это нормированная сигма-аддитивная мера на некоторой сигма-алгебре, а сигма-алгебра - это система подмножеств, которая... Нужна ли теория множеств для изучения теории вероятностей?
Топологическое пространство - это множество и система его подмножеств, которое... Нужна ли теория множеств для изучения общей топологии?
И т.д. и т.п., в математике чуть ли не каждое базовое определение начинается с "возьмем множество". Обычно никто не оговаривает, какой теории множеств подчиняется это множество.
Известно, что не все теоремы алгебры или анализа могут быть формализованы в ZF, поскольку некоторые требуют еще и аксиомы выбора. Например, теорема о том, что всякая система линейно независимых векторов может быть дополнена до базиса, и наоборот, всякая система такая, что пространство является ее линейной оболочкой, может быть обрезана до базиса. См. Halpern J.D. Bases in vector spaces and the axiom of choice // Proc. Amer. Math. Soc. 17 (1966), 670-673.
http://www.ams.org/journals/proc/1966-0 ... 4340-1.pdf. Вероятно, не все подобные вопросы еще решены, т.к. никто не провел полную формализацию теорем той же линейной алгебры в какой-нибудь теории множеств. По сути, математики полагаются на то, что их рассуждения при необходимости можно будет формализовать в какой-нибудь разумной системе оснований, например, той же ZFC.