У меня есть симметричная положительно определённая матрица
G (полученная умножением транспонированной матрицы
A на себя, но не суть):

а так же матрица
C небольшого количества ортонормированных столбцов, образующих вместе со столбцами матрицы
D ортогональную матрицу
B базисных столбцов всего пространства (
I — единичная):
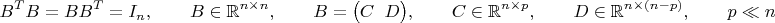
То есть, данная по условию матрица
C задаёт одно подпространство, а матрица
D — другое, ортогональное первому, но в котором надо работать.
Вопрос такой: как красиво посчитать матрицу:

Дело в том, что исходными данными для расчёта искомой матрицы
H являются матрицы
C и
G. Но в явную формулу для
H входит промежуточная величина — матрица
D, которая рассчитывается по матрице
C, причём неоднозначно. Если взять произвольную обратимую матрицу
Q и с помощью неё от
D перейти к новой
D', то формула не изменится:
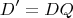
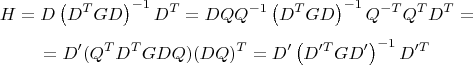
То есть матрица
H инвариантна относительно выбора
D, причём даже не обязательно, чтобы последняя была ортонормированная. Хотелось бы от этой избыточности в расчёте избавиться. Так же факт того, что число столбцов
p матрицы
C много меньше размерности пространства
n, намекает на то, что использование матрицы
D в расчёте
H довольно нерационально.
Я уже долго пытаюсь придумать, как выразить
H только через
G и
C, но ничего вразумительного пока не получается. Один тривиальный случай, когда матрица
G является единичной решается легко:
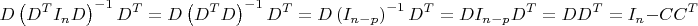
Последнее равенство следует из разложения для
B:

Ещё я пробовал посмотреть что получится для
H при попытке представить её в виде спектрального разложения, но что-то ничего путного не приходит в голову. Ну, кроме того, что у неё есть кратное (кратности
p) нулевое собственное значение и соответствующее ему подпространство, задаваемое столбцами матрицы
C.
Следующее, что мне приходит в голову — это попытаться прикрутить
формулу Шермана-Моррисона для модифицированной обратной матрицы. Но эта формула подразумевает, что обе матрицы — исходная и обратная — являются невырожденными, что в моём случае неверно: уменьшение размерности
G при переходе к
H означает зануление пачки строк и столбцов. Это означает, что эту формулу надо сначала допилить до чего-то псевдообратного в духе Мура-Пенроуза.
Подскажите, пожалуйста, что ещё можно придумать, чтобы выразить
H через
C и
G? Может я пропустил/не заметил что-то очевидное, например в спектральном разложении?

 а так же матрица
а так же матрица 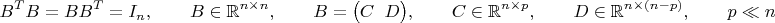 То есть, данная по условию матрица
То есть, данная по условию матрица 
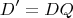
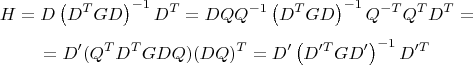 То есть матрица
То есть матрица 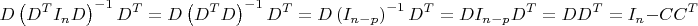 Последнее равенство следует из разложения для
Последнее равенство следует из разложения для 
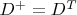
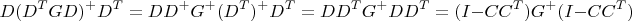
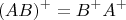 Она иногда работает, а иногда нет:
Она иногда работает, а иногда нет: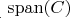 как
как 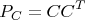 и воспользовавшись формулами по ссылке выше (не особо вникая что там происходит), у меня получилось что-то такое:
и воспользовавшись формулами по ссылке выше (не особо вникая что там происходит), у меня получилось что-то такое: 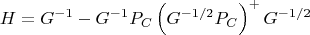 При этом требуется, чтобы G была положительно определена. При экспериментальной проверке эта формула даже работает:
При этом требуется, чтобы G была положительно определена. При экспериментальной проверке эта формула даже работает: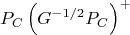 можно упростить до
можно упростить до 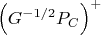 потому что эти два выражения равны. Пока не понимаю, почему это происходит и всегда ли оно так. Прямое какое-то волшебство.
потому что эти два выражения равны. Пока не понимаю, почему это происходит и всегда ли оно так. Прямое какое-то волшебство.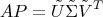
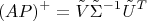 Умножение на
Умножение на 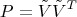 Это верно, даже если проектор до этого задавался каким-то другим базисом
Это верно, даже если проектор до этого задавался каким-то другим базисом 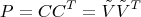 Но это не значит, что матрицы
Но это не значит, что матрицы 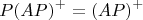 Это верно всегда, даже если матрица
Это верно всегда, даже если матрица 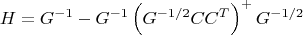
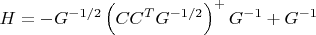
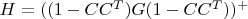 . Если не ошибся опять, напишу вывод.
. Если не ошибся опять, напишу вывод.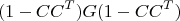 в базисе, заданном столбцами матрицы
в базисе, заданном столбцами матрицы 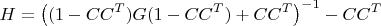 Подробнее я расписал
Подробнее я расписал  лучше?)
лучше?)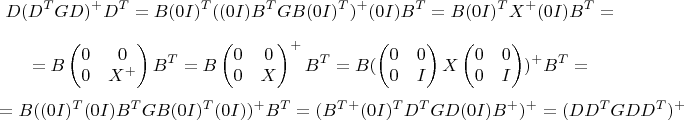
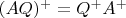 для ортогональной
для ортогональной  .
.